Uncertainty of the Standard Deviation

[a1234]

Homework Statement

I'm trying to find the uncertainty of the standard deviation of N data points, which have a Gaussian distribution. Each data point has uncertainty σ_i.

Relevant Equations

Error propagation of data that follows a Gaussian distribution, standard deviation for a sample

Using this error propagation formula:

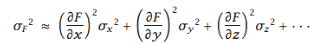
I expressed the standard deviation (s) and the partial derivatives of s w.r.t. each data point as:

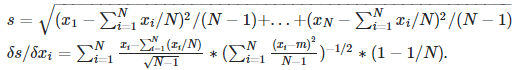
This gives me an uncertainty of:

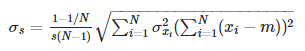, where m is the mean. Does this seem reasonable for the uncertainty of the standard deviation? I also found the thread linked below, and it looks like my formula matches the one in the thread, except for an extra factor of 1 -1/N.
https://math.stackexchange.com/questions/2439810/uncertainty-in-standard-deviation

 

[hutchphd]

You do realize that $$1-1/N =\frac {N-1} N$$and several other simplifications are available. I believe your method gives the exactly correct answer although it is really only approximate. It is difficult to know what your prof wanted because you have paraphrased the question.
Your method is not the one I would have chosen. For instance the fact that the probabilities are independent then the product of the individual probabilities yields the result more directly.

 

[a1234]

Could you explain how the result is approximate?

The instructor wanted us to use the error propagation formula specified to find the uncertainty in the standard deviation, so I believe they expected us to use this method.

Would it be possible to get rid of the second summation term under the radical sign?

 

[hutchphd]

It is approximate because the Taylor expansion is approximate. It is usually a good approximation and serves very well. I have never seen this done this way and found it an interesting exercise.
I would like to see the exact statement of the problem however.