Math Amateur
Gold Member
MHB
- 3,920
- 48
I am not sure of the overall purpose of the concepts developed below regarding Riemann integrable functions with compact support ... nor am I sure of the details ... so I am sketching out the meaning as I understand it in 2 dimensions and depicting the relevant entities in diagrams ... I am hoping that someone can indicate that my interpretation of the ideas is correct and/or point out misinterpretations, shortcomings and errors ...
On D&K pages 427 and 428 we find the following text concerning Riemann integrable functions with compact support ... note that I am assuming the overall purpose of developing the notion of Riemann integrable functions with compact support is to create the linear space of Theorem 6.2.8 together with the other results of the theorem ...


To try to ensure that I understand the details I am translating the text into the two dimensional case and briefly explaining how I interpret the text ... I also attempt to depict the ideas in diagrams ...
As I said above ... I am hoping that someone can indicate that my interpretation of the ideas is correct and/or point out misinterpretations, shortcomings and errors ...Now ... we let [math] f : \mathbb{R^2} \to \mathbb{R} [/math] be a function such that:
[math] f [/math] is bounded on [math] \mathbb{R^2} [/math] and zero outside a bounded subset [math] A \subset \mathbb{R^2} [/math]
This situation is depicted in Figure 1 below ...
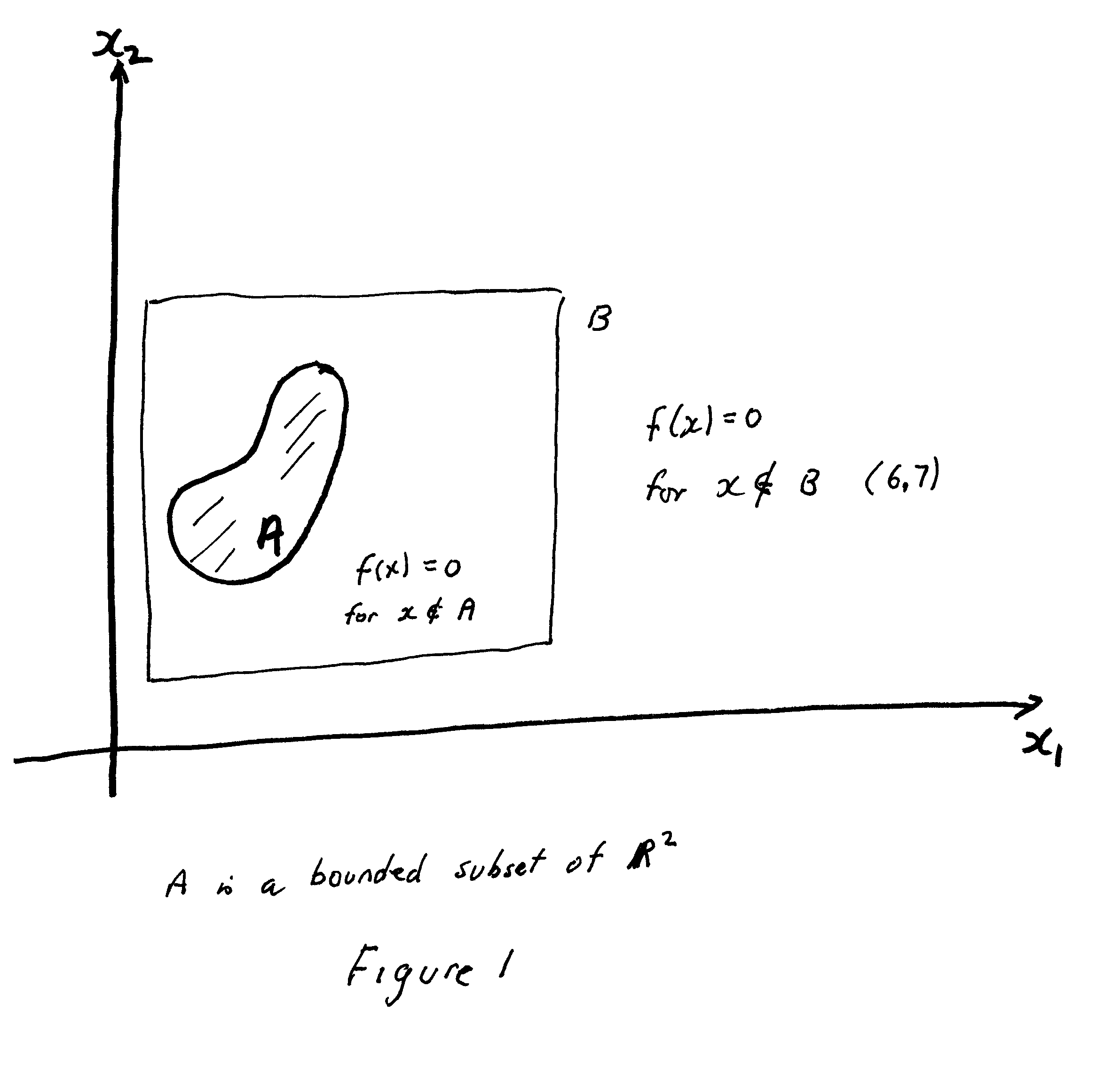 Does Figure 1 correctly and validly depict the situation described in the scanned text above from D&K ...?
Does Figure 1 correctly and validly depict the situation described in the scanned text above from D&K ...?
Now ... let B' be another rectangle satisfying (6.7) ... ... ... ... ... see Figure 2 below ...
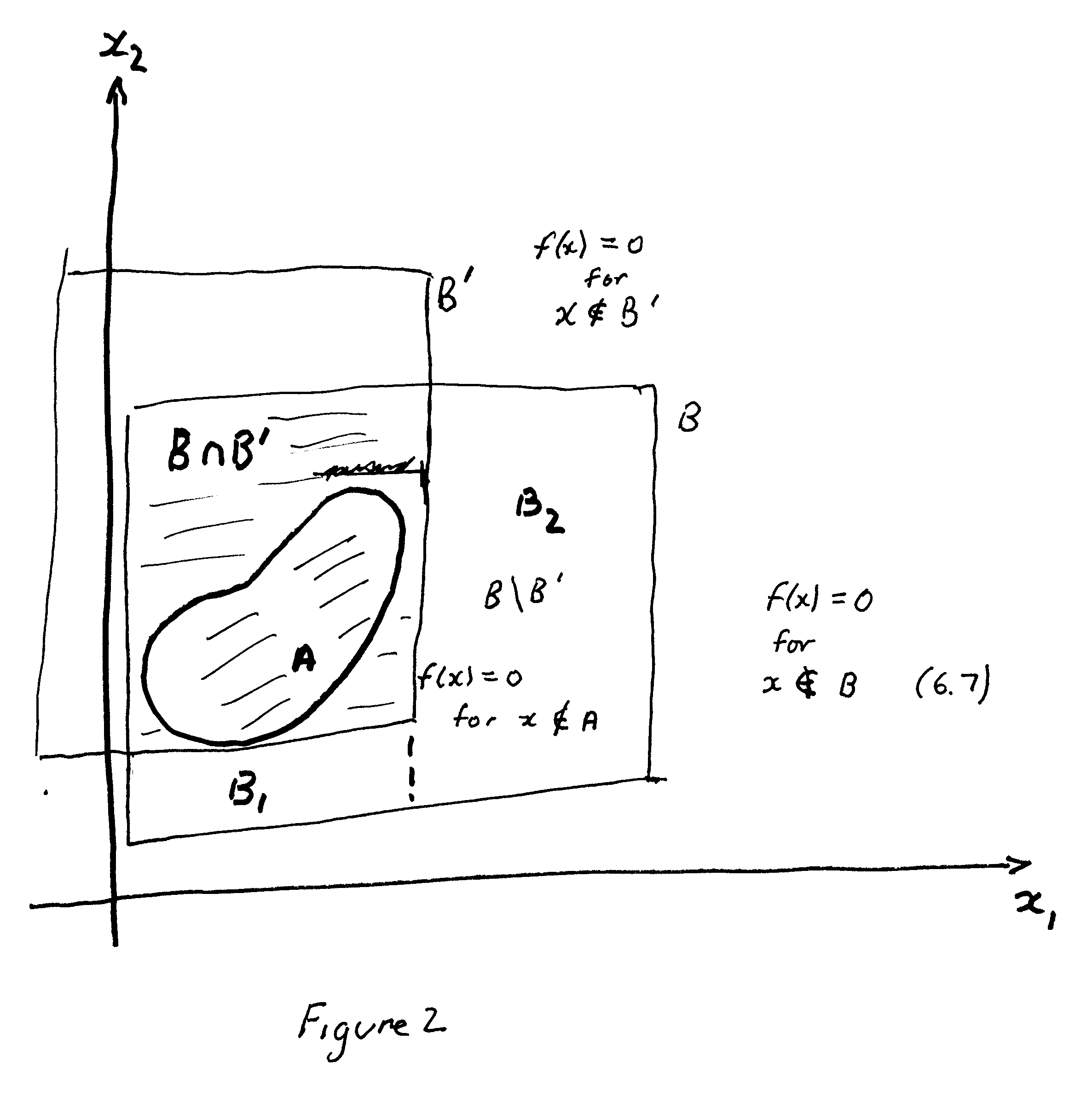 In Figure 2 clearly [math] B = (B \cap B' ) \cup ( B \text{ \ } B' ) [/math]
In Figure 2 clearly [math] B = (B \cap B' ) \cup ( B \text{ \ } B' ) [/math]
[math] B \cap B' [/math] is a two dimensional rectangle
and
[math] B \text{ \ } B' = B_1 \cup B_2 [/math]Consequently [math] \{ B \cap B' \} \cup \{ B_i \ | \ i = 1,2 \} [/math] is a partition of B ... ...We have [math] \int_{ B_i } f(x) dx \text{ for } i = 1, 2 \text{ because } f(x) =0 \text{ for } x = \text{ int}(B_i) \subset \mathbb{R^2} \text{ \ } B' [/math] ... ...But ... why isn't [math] \int_{ B_i } f(x) dx [/math] zero for the boundary of the [math] B_i [/math] as well ... ?
Is the above a correct interpretation of D&K's text as scanned above?Help will be appreciatedPeter
On D&K pages 427 and 428 we find the following text concerning Riemann integrable functions with compact support ... note that I am assuming the overall purpose of developing the notion of Riemann integrable functions with compact support is to create the linear space of Theorem 6.2.8 together with the other results of the theorem ...
To try to ensure that I understand the details I am translating the text into the two dimensional case and briefly explaining how I interpret the text ... I also attempt to depict the ideas in diagrams ...
As I said above ... I am hoping that someone can indicate that my interpretation of the ideas is correct and/or point out misinterpretations, shortcomings and errors ...Now ... we let [math] f : \mathbb{R^2} \to \mathbb{R} [/math] be a function such that:
[math] f [/math] is bounded on [math] \mathbb{R^2} [/math] and zero outside a bounded subset [math] A \subset \mathbb{R^2} [/math]
... then there exists a rectangle [math] B \subset \mathbb{R^2} [/math] with [math] f(x) = 0 \text{ if } x \notin B [/math]
( ... presumably [math] f(x) =0 [/math] for those [math] x [/math] that are inside [math] B [/math] and outside [math] A [/math] ... ... Is that correct? )
If [math] f [/math] is Riemann integrable over [math] B [/math] , the number [math] \int_B f(x) dx [/math] is independent of the choice of B ... since it only depends on A ... and other rectangles such as B' containing A will give the same result ... that is [math] \int_B f(x) dx [/math] = [math] \int_{B'} f(x) dx [/math] ... since the only non-zero values of f are coming from the set A which is in all rectangles satisfying (6.7) ... ... ... Is that correct?This situation is depicted in Figure 1 below ...
Now ... let B' be another rectangle satisfying (6.7) ... ... ... ... ... see Figure 2 below ...
[math] B \cap B' [/math] is a two dimensional rectangle
and
[math] B \text{ \ } B' = B_1 \cup B_2 [/math]Consequently [math] \{ B \cap B' \} \cup \{ B_i \ | \ i = 1,2 \} [/math] is a partition of B ... ...We have [math] \int_{ B_i } f(x) dx \text{ for } i = 1, 2 \text{ because } f(x) =0 \text{ for } x = \text{ int}(B_i) \subset \mathbb{R^2} \text{ \ } B' [/math] ... ...But ... why isn't [math] \int_{ B_i } f(x) dx [/math] zero for the boundary of the [math] B_i [/math] as well ... ?
Is the above a correct interpretation of D&K's text as scanned above?Help will be appreciatedPeter
Last edited: