- #36
chisigma
Gold Member
MHB
- 1,628
- 0
Re: Unsolved statistic questions from other sites, part II
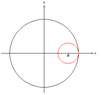
Clearly a 'direct' attack to this problem is a little unconfortable so that I'll try and 'indirect' attack. Let's suppose that the circle is the unit circle and that a 'circumcentre point' can be represented by the distance r from the point [0,0], as il the figure... View attachment 549
If we fix the circumcentre, then the mesure of the set of possible 'random points' is the area of the 'red circle' in the figure, so that the requested probability is given by the 'simple' computation...
$\displaystyle P = \int_{0}^{1} (1-r)^{2}\ d r = \frac{1}{3}$ (1)
Honestly however I'm not 'fully certain' of my solution and some suggestion and/or comments from MHB members is wellcome... Kind regards chi sigma
chisigma said:Posted on 12 15 2012 on www.artofproblemsolving.com by the member BlackMax and not yet solved...
Three points are uniformly and independently chosen inside a given circle. What is the probability that their circumcircle lies entirely within the given circle?... a C++ program suggests that the answer is most likely to be .4 ...
Clearly a 'direct' attack to this problem is a little unconfortable so that I'll try and 'indirect' attack. Let's suppose that the circle is the unit circle and that a 'circumcentre point' can be represented by the distance r from the point [0,0], as il the figure... View attachment 549
If we fix the circumcentre, then the mesure of the set of possible 'random points' is the area of the 'red circle' in the figure, so that the requested probability is given by the 'simple' computation...
$\displaystyle P = \int_{0}^{1} (1-r)^{2}\ d r = \frac{1}{3}$ (1)
Honestly however I'm not 'fully certain' of my solution and some suggestion and/or comments from MHB members is wellcome... Kind regards chi sigma