messier992
- 8
- 0
- Homework Statement
- What conditions for usage of the general specific heats?
- Relevant Equations
- u2-u1=~Cv0(T2-T1)
h2-h1=~Cp0(T2-T1)
Cv=du/DT at constant volume
Cp=dh/dT at constant Pressure
Q-W=me*he-mi*hi+m2*u
1. I am rather confused about the usage of Cp0 and Cv0 in the solutions to the question below:
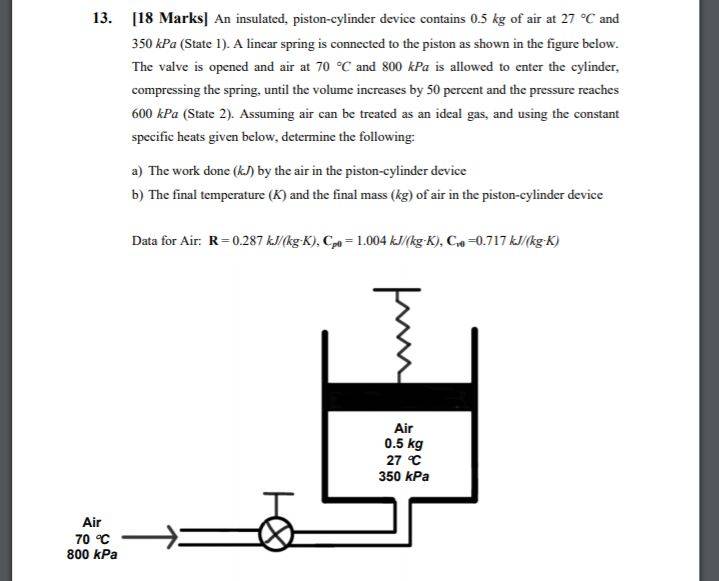
In the solution to the depicted question, the solution involves setting up the equation as follows:
Q-W=me*he-mi*hi+m2*ue-m1*u1
-W=-mi*Cp*Ti+m2CvT2-m1CvT1
I don't follow for the second step. How can the transformation of hi, u1, and u2 be valid? I thought the relation between Cp0 and Cv0 only held over an interval due to the nature of the derivation of the equations:
Cv=δu/δT at constant volume => ∫Cvδu=∫δT => u2-u1=~Cv0(T2-T1)
Cp=δh/δT at constant Pressure = ∫Cvδu=∫δT => h2-h1=~Cp0(T2-T1)2. Additionally, what are the conditions for the usage of these equations?
u2-u1=~Cv0(T2-T1)
h2-h1=~Cp0(T2-T1)
I thought they were only valid at constant volume and pressure? In the case above, the pressure/volume changes linearly, are the relations still valid then?
Lastly, mass is also added between states 1 and 2, in the case above. I understand the equation relates specific terms, per unit mass, but does this addition of mass pose a problem?
In the solution to the depicted question, the solution involves setting up the equation as follows:
Q-W=me*he-mi*hi+m2*ue-m1*u1
-W=-mi*Cp*Ti+m2CvT2-m1CvT1
I don't follow for the second step. How can the transformation of hi, u1, and u2 be valid? I thought the relation between Cp0 and Cv0 only held over an interval due to the nature of the derivation of the equations:
Cv=δu/δT at constant volume => ∫Cvδu=∫δT => u2-u1=~Cv0(T2-T1)
Cp=δh/δT at constant Pressure = ∫Cvδu=∫δT => h2-h1=~Cp0(T2-T1)2. Additionally, what are the conditions for the usage of these equations?
u2-u1=~Cv0(T2-T1)
h2-h1=~Cp0(T2-T1)
I thought they were only valid at constant volume and pressure? In the case above, the pressure/volume changes linearly, are the relations still valid then?
Lastly, mass is also added between states 1 and 2, in the case above. I understand the equation relates specific terms, per unit mass, but does this addition of mass pose a problem?
Last edited: