Using line equations to calculate a difference in rates of development

[jakerm1995]

I have two line equations representing two temperatures:

Temperature 25C: y= 0.7479x + 0.6586
Temperature 33C: y= 1.050x + 1.601

I am tasked with using these to work out the difference in development rates of a particular species under each temperature. Y= development time and x=Time. I am confused with how to use these two equations to calculate the difference in growth rate. As when I apply a percentage increase calculation to temperature 33, I calculate an 87% increase over 10 hours, and with the 25C i see a 92% increase over 10 hours. It should be that the 33C has a higher development rate and so my calculations must be wrong :/ I am very confused. I will post the graph here so you can understand better. Any suggestions are much appreciated (bare in mind, I am a noob at maths).

 

[pbuk]

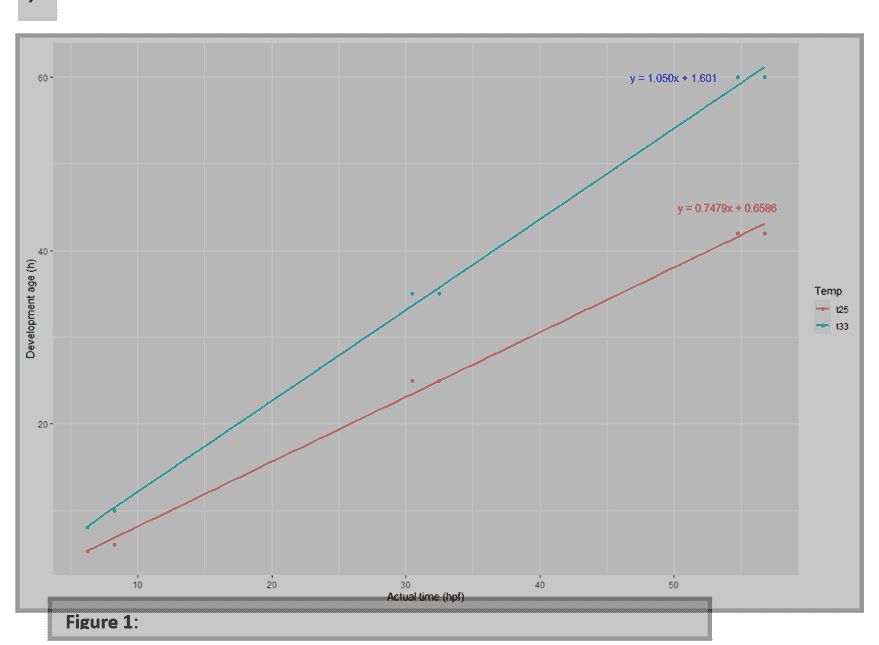
Temperature 25C: y= 0.7479x + 0.6586
Temperature 33C: y= 1.050x + 1.601

These are linear equations (i.e. they look like straight lines on the graph). The first one can be interpreted as "at 25°C every hour of real time increases developmental age by 0.7479 hours".

Percentage increases for linear equations are not constant so we can't use these, instead we can compare them by using the slope of the line, which is the coefficient of x in these equations (0.7479 development hours per hour at 25°C and 1.050 development hours per hour at 33°C). We can say that the development rate at 33°C is $\frac{1.050}{0.7479} \approx 1.404$ times that at 25°C,