Volume Generated by Rotating Two Curves About x-Axis

[jack1234]

A question here:
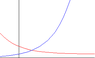
Given two curves
y=e^x
y=1+2e^(-x)

The region in the first quadrant that is bounded by the y-axis and these two curves is rotated through one complete revolution about the x-axis. Calculate the exact volume of the solid generated.

My problem is, in the first quadrant, y=1+2e^(-x) seems touching the x-axis at x=\infty, so how do we find the volume?

 

[maverick280857]

You sure you copied the problem correctly?

 

[jack1234]

Thanks, you are right that the question has not been copied correctly. I have changed
y=1+2e^(x)
to
y=1+2e^(-x)
Please refer to the original question again. Very sorry for any inconvenience caused.

 

[HallsofIvy]

The two curves cross at (0,3), of course, and the region under the two curves is symmetric about the y-axis. However, if that really is the correct formula, because y goes to 1 as x goes to \infty, and as x goes to -\infty, the volume generated contains an infinitely long cylinder of radius 1 and so is not finite.

 

[benorin]

A start

The two curves are y=e^{x} and y=1+2e^{-x} which intersect when e^{x}=1+2e^{-x} multiply by e^x to get e^{2x}-e^{x}-2=0 so by the quadratic formula we have e^{x}=2 or x = \log {2} so the curves meet at the point (log 2, 2). The other boundary is the y-axis so the bounded area is now finite (see attached plot) and to be rotated about the x-axis, so do an integral . --Ben