gloo
- 261
- 2
In the diagram I included, I was curious as to a this situation.
The columns of water are all connected and there is a hollow object that is buoyant and it's walls hug up against the walls of the left side of the 2 middle columns so that no water cannot pass between the two walls --- the hollow object can slide up and down the column.
My question is - since the far right column has a higher height of water (thus higher pressure), in a normal situation (without the hollow object present) the water on the right will push through to the left column and the water in the far left column would rise to the level "A". But with the hollow object placed where it is -- there is no difference? Even though the object is hollow, it will be pushed down by the greater water pressure on the far right column until the water in the left column rises to level "A"?
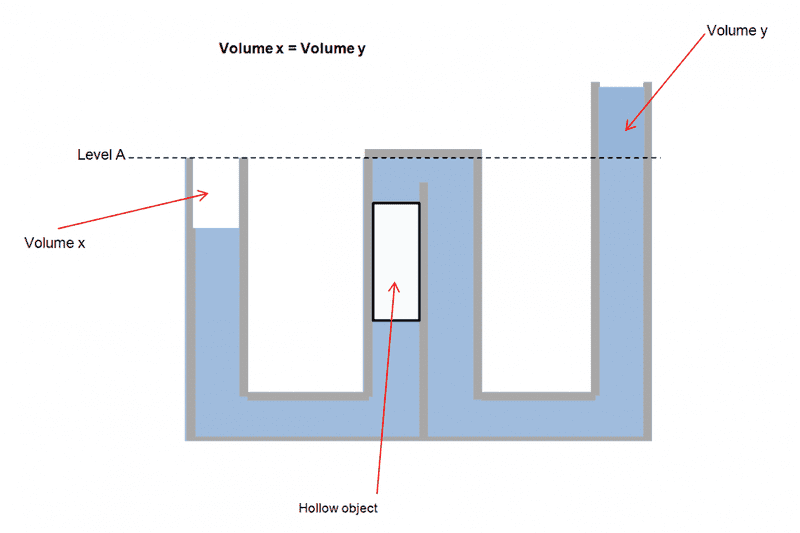
The columns of water are all connected and there is a hollow object that is buoyant and it's walls hug up against the walls of the left side of the 2 middle columns so that no water cannot pass between the two walls --- the hollow object can slide up and down the column.
My question is - since the far right column has a higher height of water (thus higher pressure), in a normal situation (without the hollow object present) the water on the right will push through to the left column and the water in the far left column would rise to the level "A". But with the hollow object placed where it is -- there is no difference? Even though the object is hollow, it will be pushed down by the greater water pressure on the far right column until the water in the left column rises to level "A"?
