NODARman
- 57
- 13
- Homework Statement
- .
- Relevant Equations
- .
Hi,
as I know the barometric formula is an exponential equation, but when I did the experiment with a barometer at different heights and inserted these results in Excel for curve fitting, it showed a weird thing, I think. So exponential equation did show that R^2=0.942 and the second-degree polynomial R^2=0.997 (the third was even .999, but that's cheating because you can solve any equation with high degrees, but anyway...).
Is that because the max height was only 15 meters and the delta pressure millibars (and not thousands of meters)?
P.S. the experiment was conducted in the "perfect-ish" environment, in the building, with the same humidity, temperature, etc.
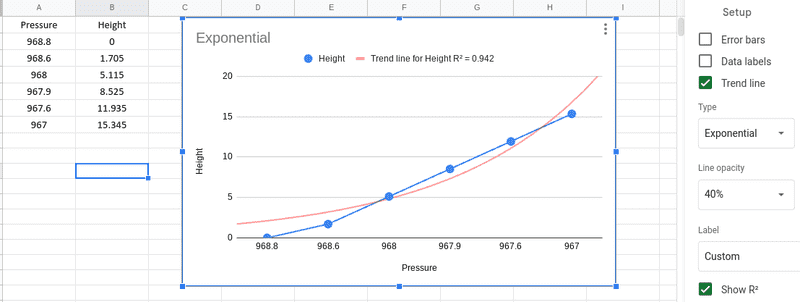
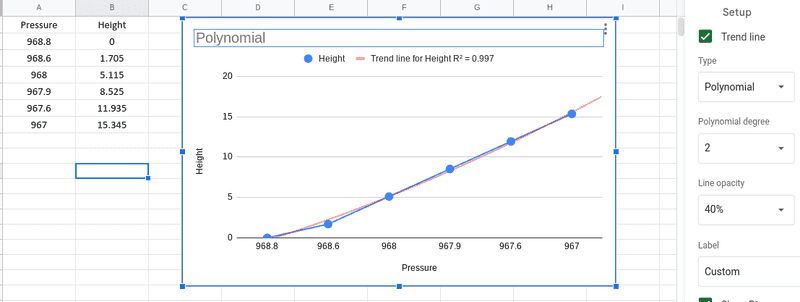
Data:
[TD]
[TR]
[TD]
[TD]
[/TR]
[TR]
[TD]
[TD]
[/TR]
[TR]
[TD]
[TD]
[/TR]
[TR]
[TD]
[TD]
[/TR]
[TR]
[TD]
[TD]
[/TR]
[TR]
[TD]
[TD]
[/TR]
as I know the barometric formula is an exponential equation, but when I did the experiment with a barometer at different heights and inserted these results in Excel for curve fitting, it showed a weird thing, I think. So exponential equation did show that R^2=0.942 and the second-degree polynomial R^2=0.997 (the third was even .999, but that's cheating because you can solve any equation with high degrees, but anyway...).
Is that because the max height was only 15 meters and the delta pressure millibars (and not thousands of meters)?
P.S. the experiment was conducted in the "perfect-ish" environment, in the building, with the same humidity, temperature, etc.
Data:
Pressure |
[TD]
Height
[/TD][TR]
[TD]
968.8
[/TD][TD]
0
[/TD][/TR]
[TR]
[TD]
968.6
[/TD][TD]
1.705
[/TD][/TR]
[TR]
[TD]
968
[/TD][TD]
5.115
[/TD][/TR]
[TR]
[TD]
967.9
[/TD][TD]
8.525
[/TD][/TR]
[TR]
[TD]
967.6
[/TD][TD]
11.935
[/TD][/TR]
[TR]
[TD]
967
[/TD][TD]
15.345
[/TD][/TR]
 ) considers these values to be labels instead of numbers
) considers these values to be labels instead of numbers