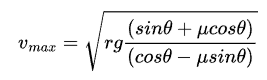First, I'm not sure where you got that this equation is for ##v_{max}##; it is for ##v## in general.
Second, the 'true' equation is:
$$\frac{v^2}{rg} = \frac{\sin\theta + \frac{f}{N}\cos\theta}{\cos\theta - \frac{f}{N}\sin\theta}$$
Where ##f## is the friction pointing down the slope, which means a negative value is possible; it only means it is going against the slope.
What is the value of ##\frac{f}{N}##? Well:
$$mg = N\cos\theta - f\sin\theta$$
Therefore:
$$\frac{f}{N} = \frac{\cos\theta - \frac{mg}{N}}{\sin\theta}$$
Note how it can have a negative value. Putting it in our original equation:
$$\frac{v^2}{rg} = \frac{\sin\theta + \left(\frac{\cos\theta - \frac{mg}{N}}{\sin\theta}\right)\cos\theta}{\cos\theta - \left(\frac{\cos\theta - \frac{mg}{N}}{\sin\theta}\right)\sin\theta}$$
Or:
$$\frac{m\frac{v^2}{r}}{N} = \sin\theta +\frac{\cos\theta - \frac{mg}{N}}{\tan\theta}$$
Isolating ##N## we get either:
$$N= \frac{m\frac{v^2}{r}\tan\theta + mg}{\sin\theta \tan\theta +\cos\theta}$$
or:
$$N = \frac{m\frac{v^2}{r} + \frac{mg}{\tan\theta}}{\sin\theta + \frac{\cos\theta}{\tan\theta}}$$
- In the first form, assuming ##\theta=0##, we get ##N=mg##.
- In the second form, assuming ##\theta = 90°##, we get ##N=m\frac{v^2}{r}##.
That's it. There is no ##v_{max}##. Whether ##\theta=0## or ##\theta=90°## or anywhere in between, you can go as fast as you want in any case. Only the normal force will change, which is independent of ##v## when ##\theta=0## and independent of ##g## when ##\theta=90°##.
But let's isolate ##\frac{f}{N}## in our original equation instead:
$$\frac{f}{N} = \frac{\frac{v^2}{rg}\cos\theta - \sin\theta}{\frac{v^2}{rg}\sin\theta + \cos\theta}$$
Or:
$$\frac{f}{N} = \frac{\frac{v^2}{rg} - \tan\theta}{\frac{v^2}{rg}\tan\theta + 1}$$
And we know that to remain static (our assumption in the first place i.e. no sliding):
$$\mu_s > \left|\frac{f}{N}\right|$$
So:
$$\mu_s > \left|\frac{\frac{v^2}{rg} - \tan\theta}{\frac{v^2}{rg}\tan\theta + 1}\right|$$
But that doesn't indicate a ##v_{min}## either, just a ##\mu_{s,\ min}##. That only means that the required friction coefficient will vary between ##\frac{v^2}{rg}## at ##\theta=0## (such that the vehicle doesn't slide out the curve) and ##\frac{rg}{v^2}## at ##\theta=90°## (such that the vehicle doesn't slide down, or "into" the curve).
The only notable thing is that if ##\frac{v^2}{rg} = \tan\theta## then ##f=0## and therefore no friction is required.We can find a ##v_{min}## and ##v_{max}## such that the vehicle doesn't begin to slide in either way.
Assuming a given ##\mu_s##, we go back to our original equation (converted to the ##\tan## equivalent):
$$\frac{v_{min}^2}{rg} = \frac{\tan\theta + (-\mu_s)}{1 - (-\mu_s)\tan\theta}$$
$$\frac{v_{max}^2}{rg} = \frac{\tan\theta + \mu_s}{1 - \mu_s\tan\theta}$$
In both cases, the right-hand side cannot be negative, so:
$$\frac{v_{min}^2}{rg} = \frac{\max\{\tan\theta; \mu_s\} - \mu_s}{1 + \mu_s\tan\theta}$$
$$\frac{v_{max}^2}{rg} = \frac{\tan\theta + \mu_s}{1 - \mu_s\min\{\tan\theta;\frac{1}{\mu_s}\}}$$
I think I got it all right.