What are the forces exerted by a wall on a hinged rod?

[bolzano95]

Homework Statement

What is the force of a wall on a revolvable rod?

Relevant Equations

II. Newton Law, Free-Body Diagram

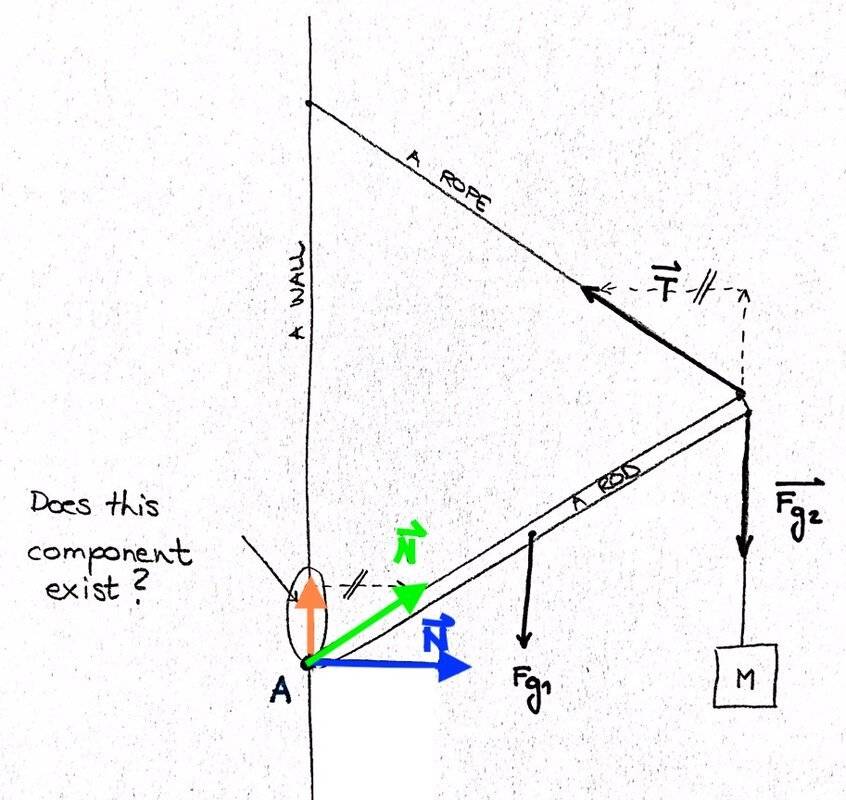
I have a dilemma.
If I look at the diagram and say the sum of the forces in x and y direction has to be zero, then I will simply conclude that the force of a wall on a revolvable rod is the blue N as drawn.

But what if the force is actually the green N? To me, it makes more sense because if imagine no tension and no mass M, then the force of a wall N would be drawn as below (green N).

So how can I argue that the orange component of N does exist? If it exists...

 

[berkeman]

You don't say it explicitly, but I'm assuming the rod is hinged at the wall contact?

What if there were no hinge there, and only friction resisted the movement of the rod in a downward direction? Can you see the vertical force in that case? What would happen to the rod if the coefficient of friction with the wall were low, like 0.1?

 

[hutchphd]

Asking whether the force "exists" is rather an odd terminology. It could exist (meaning the wall is capable of providing such a force) and yet still be zero (which is not true in this case). Which is @berkeman point. You need to solve the equations.

 

[Lnewqban]

You could also use the concept of truss, since the points of the three elements (rope, rod and wall) forming your loaded structure are not rigid but each of those allows planar rotation of one member respect to the next one.

Copied from
https://en.m.wikipedia.org/wiki/Truss

"... trusses typically comprise five or more triangular units constructed with straight members whose ends are connected at joints referred to as nodes.
In this typical context, external forces and reactions to those forces are considered to act only at the nodes and result in forces in the members that are either tensile or compressive. For straight members, moments (torques) are explicitly excluded because, and only because, all the joints in a truss are treated as revolutes, as is necessary for the links to be two-force members."

 

[bolzano95]

You don't say it explicitly, but I'm assuming the rod is hinged at the wall contact?

What if there were no hinge there, and only friction resisted the movement of the rod in a downward direction? Can you see the vertical force in that case? What would happen to the rod if the coefficient of friction with the wall were low, like 0.1?

Yes, the rod is hinged at point A.

If there were no hinge and the friction coefficient would be low, then I would conclude that the only force of a wall acting on a rod is perpendicular to a wall ------> blue N.

But this example poses a doubt: the situation is almost similar, only in this case the rod is directed downwards.
In this case the red N is correct (from the solution manual ).

But why? Is maybe the official solution wrong?

 

[hutchphd]

You need to solve the problem, allowing for a nonzero $F_{parallel}$. You can show that for a particular value of the rod angle $F_{parallel}$ will be zero if the rod has mass. If the rod were massless then the rod would be horizontal. Do you know how to solve the problem (the diagram is quite good)?

 

[bolzano95]

You need to solve the problem, allowing for a nonzero $F_{parallel}$. You can show that for a particular value of the rod angle $F_{parallel}$ will be zero if the rod has mass. If the rod were massless then the rod would be horizontal. Do you know how to solve the problem (the diagram is quite good)?

Yes, then it's quite simple.
But what about if the rod is directed downwards as the picture is shown above?

 

[hutchphd]

Solve the general problem. ($\Sigma$ torque, $\Sigma$ force, equals zero for arbitrary angle. The solution will tell you the angle required.

 

[bolzano95]

I knew it guys! The solution in the 2nd image is wrong! Got it now. Thank you for your help.

 

[hutchphd]

The image is correct. Having not seen the "solution" I cannot comment (and have no idea what you are talking about ! ).

 

[haruspex]

View attachment 281727But why? Is maybe the official solution wrong?

Note that there are just three forces on the rod. If the net torque is zero, the lines of action of the three must pass through a single point. (Do you see why?) You can use this to make more accurate diagrams.

 

[bolzano95]

The image is correct. Having not seen the "solution" I cannot comment (and have no idea what you are talking about ! ).

I meant this example:

You don't say it explicitly, but I'm assuming the rod is hinged at the wall contact?

What if there were no hinge there, and only friction resisted the movement of the rod in a downward direction? Can you see the vertical force in that case? What would happen to the rod if the coefficient of friction with the wall were low, like 0.1?

The correct solution here as well is the dark blue N, because all forces have to cancel out in the diagram.

I was confused because there was a mistake in solution manual and I wanted to be sure if I understand the normal force acting on the rod.

 

[haruspex]

I meant this example:
View attachment 281847

The correct solution here as well is the dark blue N, because all forces have to cancel out in the diagram.

I was confused because there was a mistake in solution manual and I wanted to be sure if I understand the normal force acting on the rod.

In the situation in the diagrams in posts #5 and #12, you cannot instantly say whether there is a vertical component to the reaction from the wall, nor in which direction it might be if there is one.
As I noted in post #11, for stasis, the three forces must act through a common point. Take the horizontal from the point of contact with the wall and the vertical through the mass centre and see where they intersect. If they intersect below the wire then the tension would exert an unbalanced anticlockwise torque on the rod, so there must be a vertically upward force from the wall; if they intersect above the wire then the force from the wall must have a downward component.

Going back to the diagram in post #1, there is the complication of the mass M. But we can combine the two weights into a single downward force somewhere between the two. Clearly this intersects the horizontal well below the wire, so there has to be a vertically upward component to the reaction from the wall.