What are the tensions in the strings of an accelerating elevator?

[cbarker1]

Dear Everyone,

A sphere is attached to the ceiling of an elevator by a string. A second sphere is attached to the first one by a second string. Both strings are of negligible mass. Here $m_1=m_2=m=3.52\text{ kg}$.

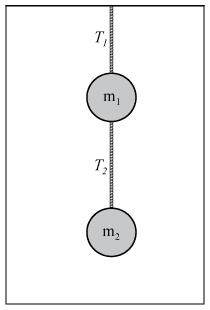
(a) The elevator starts from rest and accelerates downward with $a=1.45\,\dfrac{\text{m}}{\text{s}^2}$. What are the tensions in the two strings?

(b) If the elevator starts from rest and accelerates upward with the same acceleration, what will be the tension in the two strings?

(c) The maximum tension the two strings can withstand is 80.0 N. What maximum upward acceleration can the elevator have without having one of the strings break?

I would need to some help to setup and find the value of Tension of the cable one.

Thanks,

Cbarker1

 

[skeeter]

(a) ...

$m_2g - T_2 = m_2 a$

$m_1g+T_2-T_1 = m_1 a$

------------------------------ sum the two scalar equations ...

$(m_1+m_2)g - T_1 = (m_1+m_2)a$

$(m_1+m_2)g - (m_1+m_2)a = T_1$

evaluate $T_1$, then determine $T_2$(b) ...

$T_1 - (m_1g + T_2) = m_1a$

$T_2 - m_2g = m_2a$

same drill ...

I'll leave part (c) for you to try