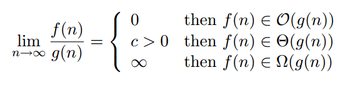shamieh
- 538
- 0
View attachment 4731
Can someone tell me if I'm even doing this correctly? I haven't dealt with TCs in while.
So I got:
$a) h_1(n) = O(n) \implies n$ , $h_2(n) = \Omega (n\log n) \implies n\log n$
$b) h_1(n) = \Omega(\log n) \implies \log n$, $h_2(n) = O(n^{2/5}) \implies n^{2/5}$
(Justification $h_1(n)$: Let $n = 1000 \implies 12(1000)^{2/3} = 524$ and Let $x = 1000 \implies 7 \log(1000) = 48$ so $n^{2/5} > \log(n)$)
(Justification $h_2(n)$: Let $n = 1000 \implies (5(100000000))^{2/5} = 3017.08..$ so $n^{2/5} > O(1)$ (or 1000) )
$c) h_1(n) = O(n^2) \implies n^2$, $h_2(n) = \Omega(n \log^4 n) \implies n \log^4 n$
$d) h_1(n) = O(\log(n)) \implies \log(n)$, $h_2(n) = \Omega (\log(n^5)) \implies \log(n^5)$
$e) h_1(n) = O(n) \implies n$, $h_2(n) = O(n) \implies n$
(Justification $h_1(n)$: let $n = 1000 \implies 1000^{1.02} = 1148.15 > \log(1000)^{1.02} = 7.17..$)
(Justification $h_2(n)$: let $n = 1000$ to find $1000(1000)log^3 1000 = 3.296.. < 2(1000) = 2000$)
$f) h_1(n) = O(n^2) \implies n^2$, $h_2(n) = \Omega(\log n) \implies \log n$
(Justification $h_1(n)$: Well $O(n^2) = n^2$ ?)
(Justification $h_2(n)$: $O(\log n) = \log n$) ?
$h) h_1(n) = O(n) \implies n$, $h_2(n) =$ exponential?
Can someone tell me if I'm even doing this correctly? I haven't dealt with TCs in while.
So I got:
$a) h_1(n) = O(n) \implies n$ , $h_2(n) = \Omega (n\log n) \implies n\log n$
$b) h_1(n) = \Omega(\log n) \implies \log n$, $h_2(n) = O(n^{2/5}) \implies n^{2/5}$
(Justification $h_1(n)$: Let $n = 1000 \implies 12(1000)^{2/3} = 524$ and Let $x = 1000 \implies 7 \log(1000) = 48$ so $n^{2/5} > \log(n)$)
(Justification $h_2(n)$: Let $n = 1000 \implies (5(100000000))^{2/5} = 3017.08..$ so $n^{2/5} > O(1)$ (or 1000) )
$c) h_1(n) = O(n^2) \implies n^2$, $h_2(n) = \Omega(n \log^4 n) \implies n \log^4 n$
$d) h_1(n) = O(\log(n)) \implies \log(n)$, $h_2(n) = \Omega (\log(n^5)) \implies \log(n^5)$
$e) h_1(n) = O(n) \implies n$, $h_2(n) = O(n) \implies n$
(Justification $h_1(n)$: let $n = 1000 \implies 1000^{1.02} = 1148.15 > \log(1000)^{1.02} = 7.17..$)
(Justification $h_2(n)$: let $n = 1000$ to find $1000(1000)log^3 1000 = 3.296.. < 2(1000) = 2000$)
$f) h_1(n) = O(n^2) \implies n^2$, $h_2(n) = \Omega(\log n) \implies \log n$
(Justification $h_1(n)$: Well $O(n^2) = n^2$ ?)
(Justification $h_2(n)$: $O(\log n) = \log n$) ?
$h) h_1(n) = O(n) \implies n$, $h_2(n) =$ exponential?
Attachments
Last edited: