What are the Variables Needed to Solve a Pulley System Problem?

[cbarker1]

Two blocks are connected by a massless rope as shown below. The mass of the block on the table is 5.4 kg and the hanging mass is 2.1 kg. The table and the pulley are frictionless.

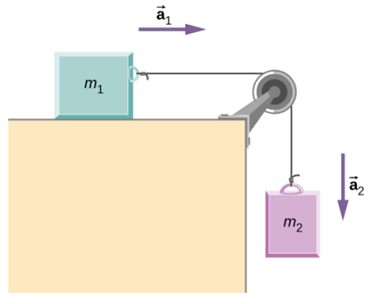I need to find acceleration, the tension of the rope, and the speed when mass 2 hits the floor when it starts from rest and is initially located 1.3 m from the floor.
I need some help with the setup.

 

[MarkFL]

Let's look at the forces on each object in turn. For $m_1$, we have:

$$\sum F_x=T=m_1a$$

And for $m_2$, we have:

$$\sum F_y=m_2g-T=m_2a$$

Now we have two equations in two unknowns...can you proceed?

To answer the second part of the question, I would use the kinematic equation:

$$\Delta y=\frac{v_f^2-v_i^2}{2a}$$

Solve that for $v_f$, and then use the given values (and the acceleration $a$ you found in the first part) to get your answer. :)

 

[MarkFL]

As a follow-up, we have when substituting for $T$ from the first equation into the second:

$$m_2g-m_1a=m_2a$$

Solving for $a$, we obtain:

$$a=\frac{m_2g}{m_1+m_2}$$

And so:

$$T=\frac{m_1m_2g}{m_1+m_2}$$

And finally:

$$v_f=\sqrt{\frac{2m_2g\Delta y}{m_1+m_2} + v_i^2}$$