- #36
PeterDonis
Mentor
- 47,601
- 23,875
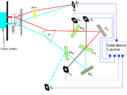
The above seems inconsistent with this:DrChinese said:They almost exactly follow classical trajectories.
The latter I would agree with; the former I would not. I don't see how both can be true (to be clear, I'm talking about the case where there are no fiber optic cables or other devices present, just free space between source and detector).DrChinese said:They are NOT classical paths
I agree with all of this.DrChinese said:photons are quantum particles, not classical particles. I don't know if an individual photon travels on one path, many paths (path integral concept), different paths in different MWI worlds, exact Bohmian trajectories, are continuous or not, etc. They can do lots of things when not being observed. (Nobody I aware of on this planet has any superior understanding of the "truth" of what happens.)
So what do you think justifies this, given the other statements quoted above?DrChinese said:every experimentalist does all test calibration as if they are observing entangled photons moving on their precisely desired "classical" path with a classically expected arrival time relative to the entangled partner.