What is a Different Method for Implicit Differentiation?

[chwala]

Homework Statement

Find the equation of the normal to a curve given parametric equations;

$x=t^3, y=t^2$

Relevant Equations

Parametric equations

This is a text book example- i noted that we may have a different way of doing it hence my post.

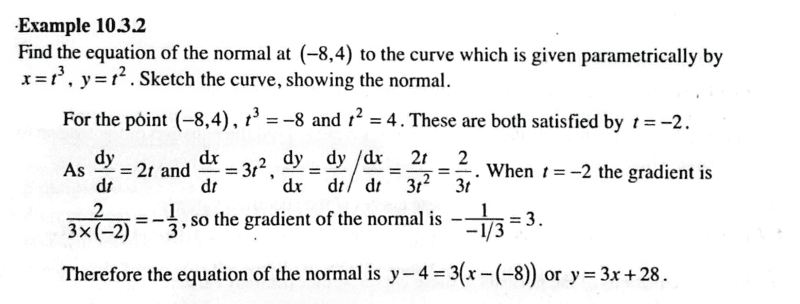
Alternative approach (using implicit differentiation);

$\dfrac{x}{y}=t$

on substituting on $y=t^2$

we get,

$y^3-x^2=0$

$3y^2\dfrac{dy}{dx}-2x=0$

$\dfrac{dy}{dx}=\dfrac{2x}{3y^2}$

at points $(-8,4)$

$\dfrac{dy}{dx}=\dfrac{-1}{3}$

...the rest of the steps to required solution will follow...

...any insight is welcome.

 

[pasmith]

Or $$\begin{split}<br /> \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} &= \begin{pmatrix} t^3 \\ t^2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 3t^2 \\ 2t \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \\<br /> &= \begin{pmatrix} t^3 \\ t^2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 2t \\ -3t^2 \\ 0 \end{pmatrix}<br /> \end{split}$$ and then $$\lambda = \frac{x - t^3}{2t} = \frac{y - t^2}{-3t^2}\quad\Rightarrow\quad<br /> y = t^2 - 3t^2\frac{x - t^3}{2t} = t^2 + \tfrac32 t^4 - \tfrac32 tx.$$

 

[Steve4Physics]

The book-solution is presumably given simply as a teaching-demonstration of how to solve this type of problem using parametric coordinates. But note, sometimes elimination of the parametric coordinates simplifies the problem. In this particular question(at the risk of stating the obvious):

$x=t^3, y= t^2 ⇒ y = x^{\frac 23}$

$\frac {dy}{dx} = \frac 23 x^{-\frac13}$

When $x = -8, \frac {dy}{dx} = \frac 23 (-8)^{-\frac13}= -\frac 13$

etc.