What Is the Angular Velocity of a Falling Mass-Driven Wheel?

[PC22]

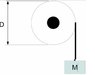
A uniform Steel wheel of diameter, D=3m and mass, 8500kg is supported by a low friction bearing, shown as the large black spot in the drawing. Around the outer surface of the wheel, a light wire rope is wound. From the end of this wire rope, a mass, M=1000kg is attached

Initially, both the wheel and the mass are at rest. The mass is released, and falls through a hight of 30m before hitting the Earth's surface. As the mass falls, the tension in the wire rope turnes the wheel, i.e., the wire rope unswinds

Homework Equations

what is the speed of the mass just before it hits the ground ? and, what is the corresponding angular velocity of the wheel?

(assume the acceleration owing to gravity is equal to 9.81m/s^2)

The Attempt at a Solution

I've had a go at both questions but I am not sure if they are right, could some one please let me know if this is correct or where I have gone wrong ?

Third equation of motion
V=U+2as
initial velocity =U=0M/s
uniformed accelleration= 9.81M/s
distance traveled =t=30m

V=u+2as
V=0+2x9.81x30


V=588.6m/s

angular velocity

ω=v/r

ω=588.6/1.5

ω=392.4r/s

 

[paisiello2]

The acceleration is not g. It would be if the steel wheel had negligible mass compared to the mass M.

But imagine if the steel wheel were extremely large and massive and the mass M were very small. Would you think intuitively that the acceleration would still be g?

 

[Delgado_72]

Hi! I don't think your answers are right.
According to the principle of conservation of energy, the the speed of the block will be as shown in the picture.
The angular speed formula is correct, the problem is the speed.
w=v/r <=> w=24.26/1.5=16.17rad/s

 

[Delgado_72]

Hope it helped!

 

[PC22]

AAAHH I'm an idiot I forgot to square root the velocity! so this is correct then??

Vroot2=u+2as
Vroot2=0+2x9.81x30
Vroot2=24.2m/s

angular velocity
ω=v/r
ω=24.2/1.5

ω=16.13r/m

 

[Delgado_72]

Yes! Now it is correct!
Keep in mind that both velocities are squared in that particular equation

 

[paisiello2]

Does the rotating wheel also have kinetic energy?

 

[Delgado_72]

K=(1/2)Iw^2

I = moment of inertia= (1/2)mr^2
w = angular speed = v/r

K=1/2*1/2*m*r^2*(v/r)^2
K=1/4*m*v^2

When an object has translational as well as rotational motion, its total kinetic energy is the sum of the translational kinetic energy and the rotational kinetic energy.Please check my calculations

 

[paisiello2]

Yes, but you didn't include this in your estimate of v for mass M.

 

[Delgado_72]

Ok let me try again.
The energy of the system must stay the same, therefore, the variation of energy of the block must be the same (symmetric) as the variation of the energy of the wheel.
The loss of potential energy of the block will result on the increase of the kinetic energy.

KE=PE
1/4mv^2=mgh
v^2=4gh
v=(4*9.81*30)^1/2
v=34,31m/s

 

[Delgado_72]

w=v/r
w=34,31/1,5
w=22,87

 

[paisiello2]

Now what happened to the translational kinetic energy? Your first attempt included it but excluded the rotational component of kinetic energy. Now for some reason you are including rotational but excluding translational.

Here is your own statement:

When an object has translational as well as rotational motion, its total kinetic energy is the sum of the translational kinetic energy and the rotational kinetic energy.

 

[Delgado_72]

But the wheel is attached isn't it? Therefore there would only be rotational kinetic energy..

 

[paisiello2]

Attached to what?

You have to look at the energy of the entire system. Or if you only want to look at the wheel then you have to consider all forces that exert work on the wheel.

 

[Delgado_72]

It says that the wheel is supported. There is no translational movement. Only rotational

 

[paisiello2]

but the mass has translational velocity, yes?

 

[Delgado_72]

But the wheel as a whole does not move through space. It only spins around it's center of mass.
Kinetic energy is only rotational.

 

[paisiello2]

Yes, but it is attached to the falling mass which has a translational kinetic energy. you have to consider the system as a whole.

 

[Delgado_72]

Yes, but when the block comes to rest, all of its translational kinetic energy is transformed into rotational kinetic energy on the wheel. That is what my previous calculations demonstrated

 

[paisiello2]

but that is not what the question asked.

and even if it did you still calculated it wrong.

 

[Delgado_72]

How so? Well then show me your work please

 

[paisiello2]

Sorry, not going to do that. But I will tell you that you are wrong because once the mass hits the ground, the wire rope goes slack effectively breaking the system up into two independent systems. Before the mass hits the ground the wire rope effectively ties the masses m and M together into one single system.

But let's not waste time discussing something that the OP didn't even ask. Why don't you attempt to answer the original question first?

 

[Delgado_72]

Calculating the acceleration of the block do you take in consideration the weight of the wheel even if translationally at rest?

 

[paisiello2]

Yes! It still has inertia that tries to resist any accelerating rotation.

See my very first post (#2) in this thread.