You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB What is the area of square ABCD with OQ = OF = 6?
AI Thread Summary
The area of square ABCD can be determined using coordinate geometry, given that OQ and OF both equal 6. By establishing a coordinate system with O at the origin, the calculations reveal that the midpoint M of line segment HK is crucial for determining the dimensions of the square. The derived relationships between the coordinates lead to the conclusion that the side length of the square is equal to the square root of 12. Consequently, the area of square ABCD is confirmed to be 12. A purely geometric solution is desired but not provided in the discussion.
Mathematics news on Phys.org
Opalg
Gold Member
MHB
- 2,778
- 13
Here is an outline of a solution using coordinate geometry.
[TIKZ][scale=1.5]
\coordinate [label=above right:{\textcolor{blue}O}] (O) at (0,0) ;
\coordinate [label=above right:{\textcolor{blue}A}] (A) at (0,3.46) ;
\coordinate [label=above right:{\textcolor{blue}B}] (B) at (1.73,0.46) ;
\coordinate [label=above right:{\textcolor{blue}C}] (C) at (4.73,2.19) ;
\coordinate [label=above right:{\textcolor{blue}D}] (D) at (3,5.2) ;
\coordinate [label=above right:{\textcolor{blue}F}] (F) at (6,0) ;
\coordinate [label=above right:{\textcolor{blue}H}] (H) at (5.91,1.02) ;
\coordinate [label=above right:{\textcolor{blue}K}] (K) at (1.02,5.91) ;
\coordinate [label=above right:{\textcolor{blue}Q}] (Q) at (0,6) ;
\coordinate [label=above right:{M}] (M) at (3.46,3.46) ;
\draw [blue, ultra thick] (A) -- (B) -- (C) -- (D) -- cycle ;
\draw [brown, ultra thick] (H) -- (K) ;
\draw [blue, ultra thick] (F) -- (O) -- (Q) ;
\draw [blue, ultra thick] (F) arc (0:90:6) ;
\draw [brown, ultra thick] (K) arc (135:315:3.46) ;
\draw [thin] (A) -- (M) -- (3.46,0) ;
\draw [thin] (K) |- (M) |- (C) ;
\draw (0.9,4.7) node {$s$} ;
\draw (2.2,3.6) node {$s$} ;
\draw (-0.2,1.7) node {$t$} ;
\draw (1.7,-0.2) node {$t$} ;
\draw (3.3,2.8) node {$u$} ;
\draw (4.1,2.1) node {$u$} ;
\draw [thin, dashed] (A) -- (C) ;
\draw [thin, dashed] (B) -- (D) ;
\foreach \point in {O,A,B,C,D,F,H,K,Q} \fill [blue] (\point) circle (2pt) ;
\fill (M) circle (2pt) ;[/TIKZ]
Choose a coordinate system with origin at O, so that F is the point $(6,0)$ and Q is $(0,6)$.
I assume that the brown part of the diagram is meant to be a semicircle and its diameter. Let M be the midpoint of HK, with coordinates $(t,t)$, so that the semicircle has radius $t$. Then the line HK has equation $x+y = 2t$. Let K be the point $(t-s,t+s)$. The distance KM is $t$, from which it follows that $t^2 = 2s^2$. The condition that K lies on the blue circle of radius $6$ is $(t+s)^2 + (t-s)^2 = 36$, from which $3t^2 = 36$ and hence $t = \sqrt{12}$.
Next, let C be the point $(t+u,t-u)$. The centre of the square ABCD is the midpoint of AC, namely $\bigl(\frac12t+ \frac12u, t - \frac12u\bigr)$. You can then calculate that B is the point $\bigl(\frac12t,\frac12t-u\bigr)$ and D is $\bigl(\frac12t + u,\frac32t\bigr)$. The conditions that B lies on the brown semicircle and that D lies on the blue circle both lead to the same equation $2u^2 + 2ut - t^2 = 0$. Therefore $u = \frac12(\sqrt3 - 1)t = 3-\sqrt3$.
Knowing $t$ and $u$, you can then easily check that the distance AB is $t$. So the area of the square ABCD is $t^2 = 12$.
I would much prefer to have a solution using a purely geometric argument, but I do not see how to do that.
[TIKZ][scale=1.5]
\coordinate [label=above right:{\textcolor{blue}O}] (O) at (0,0) ;
\coordinate [label=above right:{\textcolor{blue}A}] (A) at (0,3.46) ;
\coordinate [label=above right:{\textcolor{blue}B}] (B) at (1.73,0.46) ;
\coordinate [label=above right:{\textcolor{blue}C}] (C) at (4.73,2.19) ;
\coordinate [label=above right:{\textcolor{blue}D}] (D) at (3,5.2) ;
\coordinate [label=above right:{\textcolor{blue}F}] (F) at (6,0) ;
\coordinate [label=above right:{\textcolor{blue}H}] (H) at (5.91,1.02) ;
\coordinate [label=above right:{\textcolor{blue}K}] (K) at (1.02,5.91) ;
\coordinate [label=above right:{\textcolor{blue}Q}] (Q) at (0,6) ;
\coordinate [label=above right:{M}] (M) at (3.46,3.46) ;
\draw [blue, ultra thick] (A) -- (B) -- (C) -- (D) -- cycle ;
\draw [brown, ultra thick] (H) -- (K) ;
\draw [blue, ultra thick] (F) -- (O) -- (Q) ;
\draw [blue, ultra thick] (F) arc (0:90:6) ;
\draw [brown, ultra thick] (K) arc (135:315:3.46) ;
\draw [thin] (A) -- (M) -- (3.46,0) ;
\draw [thin] (K) |- (M) |- (C) ;
\draw (0.9,4.7) node {$s$} ;
\draw (2.2,3.6) node {$s$} ;
\draw (-0.2,1.7) node {$t$} ;
\draw (1.7,-0.2) node {$t$} ;
\draw (3.3,2.8) node {$u$} ;
\draw (4.1,2.1) node {$u$} ;
\draw [thin, dashed] (A) -- (C) ;
\draw [thin, dashed] (B) -- (D) ;
\foreach \point in {O,A,B,C,D,F,H,K,Q} \fill [blue] (\point) circle (2pt) ;
\fill (M) circle (2pt) ;[/TIKZ]
Choose a coordinate system with origin at O, so that F is the point $(6,0)$ and Q is $(0,6)$.
I assume that the brown part of the diagram is meant to be a semicircle and its diameter. Let M be the midpoint of HK, with coordinates $(t,t)$, so that the semicircle has radius $t$. Then the line HK has equation $x+y = 2t$. Let K be the point $(t-s,t+s)$. The distance KM is $t$, from which it follows that $t^2 = 2s^2$. The condition that K lies on the blue circle of radius $6$ is $(t+s)^2 + (t-s)^2 = 36$, from which $3t^2 = 36$ and hence $t = \sqrt{12}$.
Next, let C be the point $(t+u,t-u)$. The centre of the square ABCD is the midpoint of AC, namely $\bigl(\frac12t+ \frac12u, t - \frac12u\bigr)$. You can then calculate that B is the point $\bigl(\frac12t,\frac12t-u\bigr)$ and D is $\bigl(\frac12t + u,\frac32t\bigr)$. The conditions that B lies on the brown semicircle and that D lies on the blue circle both lead to the same equation $2u^2 + 2ut - t^2 = 0$. Therefore $u = \frac12(\sqrt3 - 1)t = 3-\sqrt3$.
Knowing $t$ and $u$, you can then easily check that the distance AB is $t$. So the area of the square ABCD is $t^2 = 12$.
I would much prefer to have a solution using a purely geometric argument, but I do not see how to do that.
maxkor
- 79
- 0
Hint:

maxkor
- 79
- 0
Solution pure geometry:
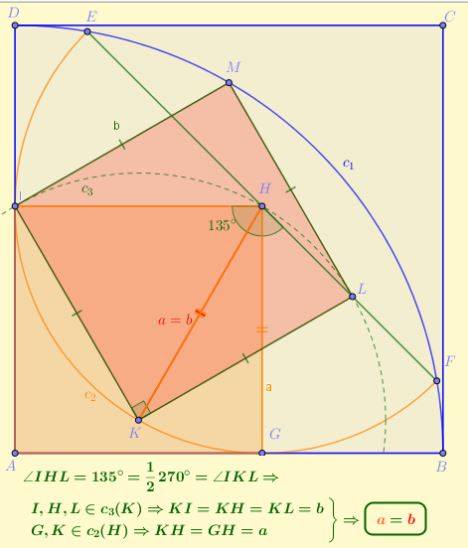
Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
Just chatting with my son about Maths and he casually mentioned that 0 would be the midpoint of the number line from -inf to +inf. I wondered whether it wouldn’t be more accurate to say there is no single midpoint. Couldn’t you make an argument that any real number is exactly halfway between -inf and +inf?
A power has two parts. Base and Exponent.
A number 423 in base 10 can be written in other bases as well:
1. 4* 10^2 + 2*10^1 + 3*10^0 = 423
2. 1*7^3 + 1*7^2 + 4*7^1 + 3*7^0 = 1143
3. 7*60^1 + 3*60^0 = 73
All three expressions are equal in quantity. But I have written the multiplier of powers to form numbers in different bases. Is this what place value system is in essence ?
Similar threads
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 6
- Views
- 1K
- Replies
- 5
- Views
- 2K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
-
I Geometry problem of interest with a 3-4-5 triangle
- Started by Charles Link
- Replies: 59
- General Math
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
