Ihsan
- 2
- 1
- Homework Statement
- 1- Find the body force b that acts on this continuum so that Cauchy’s first equation of motion.
2-Find the body forces at the reference point ( 1, 2, 1) where ρ0(rho nod)= 2
- Relevant Equations
- Balance of Linear Momentum or Cauchy first equation of motion -->b+div σ =ρ x ( x here div x and again div x two time)
Hi,
unfortunately, I am not getting anywhere with the following task
and I try solve it
unfortunately, I am not getting anywhere with the following task
and I try solve it
Attachments
-
 لقطة شاشة 2023-12-16 010246.png22.8 KB · Views: 98
لقطة شاشة 2023-12-16 010246.png22.8 KB · Views: 98 -
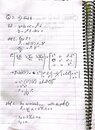 WhatsApp Image 2023-12-16 at 12.20.18 AM.jpeg55 KB · Views: 71
WhatsApp Image 2023-12-16 at 12.20.18 AM.jpeg55 KB · Views: 71 -
 WhatsApp Image 2023-12-16 at 12.20.17 AM (1).jpeg24.6 KB · Views: 71
WhatsApp Image 2023-12-16 at 12.20.17 AM (1).jpeg24.6 KB · Views: 71 -
 WhatsApp Image 2023-12-16 at 12.20.17 AM.jpeg46.4 KB · Views: 88
WhatsApp Image 2023-12-16 at 12.20.17 AM.jpeg46.4 KB · Views: 88 -
 WhatsApp Image 2023-12-16 at 12.20.15 AM.jpeg41.1 KB · Views: 70
WhatsApp Image 2023-12-16 at 12.20.15 AM.jpeg41.1 KB · Views: 70