kshitij
- 218
- 27
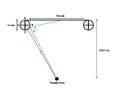
I'll have to disagree on that one, I think the limiting case should look like this,haruspex said:Yes, that's the picture I have in mind.
If you set theta to zero and increase x a bit (it is less than R/sqrt(2) in your example) it will make a glancing blow on the post and continue towards the goal line. It will be a goal if the other post is sufficiently far away.
kshitij said:Homework Statement:: Consider two shapes of goal posts, one with a circular cross-section and the other with square. Which of these posts have a greater probability of a shot hitting the post, go in?
Relevant Equations:: Laws of reflection
Limiting/critical incidence,
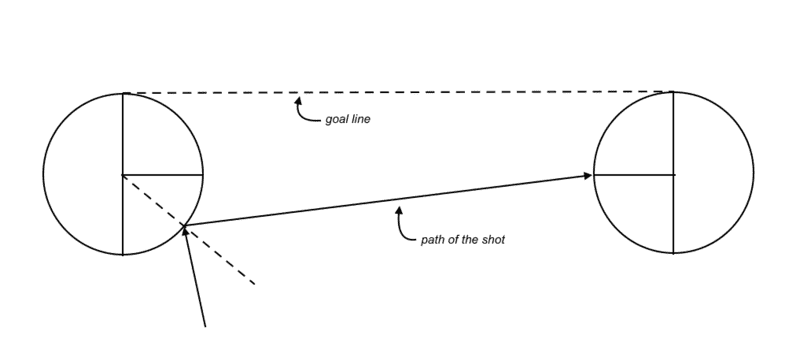
kshitij said:Homework Statement:: Consider two shapes of goal posts, one with a circular cross-section and the other with square. Which of these posts have a greater probability of a shot hitting the post, go in?
Relevant Equations:: Laws of reflection
The critical value of angle of incidence happens when the reflected ray from the sector BC of one post hits the sector AB of the other post.