- #1
MHB What is the correct formula for calculating savings plan?
- Thread starter Ladybug101
- Start date
-
- Tags
- Plan Word problem
Click For Summary
The correct formulas for calculating a savings plan depend on when deposits are made: at the end of the month or the beginning. For end-of-month deposits, use the formula S_Ordinary = p[(1 + r/n)^(ny) - 1] / (r/n). For beginning-of-month deposits, the formula is S_Due = p[(1 + r/n)^(ny) - 1] / (r/n) * (1 + r/n). The choice between these formulas affects the future value of the savings plan. Clarifying the timing of deposits is essential for accurate calculations.
- #2
jonah1
- 107
- 0
Beer induced opinions follow. In no event shall the wandering math knight-errant Sir jonah in his inebriated state be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of his beer inspired views.
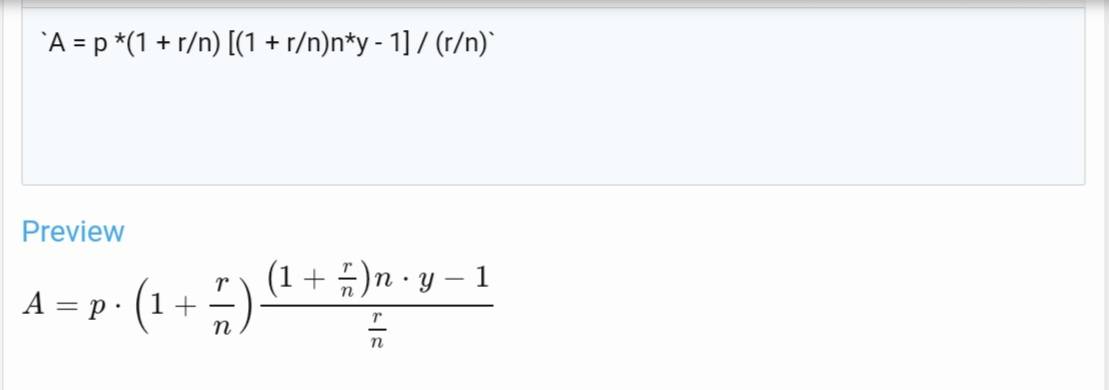
Alas Milady, that formula you gave is incorrect.
That should either be
$$S_{Ordinary}=p\frac{\left(1+\frac{r}{n}\right)^{ny}-1}{\frac{r}{n}}$$
OR
$$S_{Due}=p\frac{\left(1+\frac{r}{n}\right)^{ny}-1}{\frac{r}{n}}\left(1+\frac{r}{n}\right)$$
where we replace $A$ (which denotes the present value) with $S$ (which denotes the future value).
It depends upon when you plan to make your monthly deposit, that is, at the end of the month (1st formula, future value of an ordinary annuity or end of period payments/deposits) or at the beginning of the month (very likely, 2nd formula, future value of an annuity due or beginning of period payments/deposits).
The question now is when do you plan to make your monthly deposits - at the beginning of the month or at the end of the month - to accumulate 30,000 at the end of 5 years. After you've made that clarification, it boils down to a mere plug and chug routine. You can try both if you like and compare the resulting $p$'s with your textbook's answer section if your problem is from a textbook.
Ladybug101 said:
Alas Milady, that formula you gave is incorrect.
That should either be
$$S_{Ordinary}=p\frac{\left(1+\frac{r}{n}\right)^{ny}-1}{\frac{r}{n}}$$
OR
$$S_{Due}=p\frac{\left(1+\frac{r}{n}\right)^{ny}-1}{\frac{r}{n}}\left(1+\frac{r}{n}\right)$$
where we replace $A$ (which denotes the present value) with $S$ (which denotes the future value).
It depends upon when you plan to make your monthly deposit, that is, at the end of the month (1st formula, future value of an ordinary annuity or end of period payments/deposits) or at the beginning of the month (very likely, 2nd formula, future value of an annuity due or beginning of period payments/deposits).
The question now is when do you plan to make your monthly deposits - at the beginning of the month or at the end of the month - to accumulate 30,000 at the end of 5 years. After you've made that clarification, it boils down to a mere plug and chug routine. You can try both if you like and compare the resulting $p$'s with your textbook's answer section if your problem is from a textbook.
Obviously, there is something elementary I am missing here.
To form the transpose of a matrix, one exchanges rows and columns, so the transpose of a scalar, considered as (or isomorphic to) a one-entry matrix, should stay the same, including if the scalar is a complex number. On the other hand, in the isomorphism between the complex plane and the real plane, a complex number a+bi corresponds to a matrix
in the real plane; taking the transpose we get
which then corresponds to a-bi...
Similar threads
- · Replies 1 ·
- · Replies 6 ·
- · Replies 2 ·
- · Replies 7 ·
- · Replies 6 ·
- · Replies 1 ·
- · Replies 4 ·
- · Replies 2 ·
- · Replies 11 ·
- · Replies 2 ·