MHB What is the correct slant asymptote for this function and why is it significant?

[m3dicat3d]

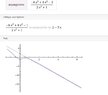
View attachment 819Why is the slant asymptote pictured here correct for this function? I was under the impression an asymptote was never crossed by the function. I get that the dividend gives the equation for the asymptote for a non zero remainder, but seeing this graphically is a bit confusing. Thanks! (EDIT: NVM, I just answered my own question:p) Thanks anyways though!

 

[Prove It]

If you long divide, you'll see that [math]\displaystyle \frac{-6x^3 + 4x^2 - 1}{2x^2 + 1} \equiv -3x + 2 + \frac{x}{2x^2 + 1} = -3x + 2 + \frac{1}{2x + \frac{1}{x}} [/math].

You can see that the denominator easily overpowers the numerator, and so gets closer to 0, which means the entire function eventually works like [math]\displaystyle -3x + 2[/math]. However, since there is always that tiny bit added, it never actually will be [math]\displaystyle -3x + 2[/math], and so [math]\displaystyle y = -3x + 2[/math] must be an asymptote :)