What is the derivative of ln(x)^e ?

[lIllIlIIIl]

Can't figure it out, here's a screenshot with better typography.

 

[jedishrfu]

Is this math homework? or something else?

EDIT: Disregard the following as I thought you were trying to integrate this expression which is very hard to do. I leave the proof to the students of the future.

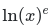
Often integral tables can help get an answer but they are acceptable when its a homework assignment. I looked at a few and this integral is not listed. They do show ones where ##ln(x)^n## with n an integer but none with a real number power.

What work have you done to solve this?

One attack that might work is to replace ln(x) with y and ask what is the integral for that and then you could use the function of a function approach to get an answer.

 

[PeroK]

Can't figure it out, here's a screenshot with better typography.
View attachment 331333

I can't imagine where that function came from, but the chain rule is your friend!

 

[vela]

I moved the thread to the homework forums since this is a homework-type problem.

 

[WWGD]

Like PeroK said, try describing your function as a composition of other functions . Then apply the Chain Rule.

 

[Mark44]

Can't figure it out, here's a screenshot with better typography.
View attachment 331333

Your problem is ambiguous, so isn't clear to me.

Is it $\ln[x^e]$ or is it $(\ln(x))^e$? IOW, are we raising x to the power e or are we raising $\ln(x)$ to the power e?

 

[Mark44]

One attack that might work is to replace ln(x) with y and ask what is the integral for that

The problem asks for the derivative, not the integral.

 

[jedishrfu]

I guess I’m not the only one with a reading problem.