Billy.Ljm
- 4
- 0
I have 2 questions, which are related, and was hoping someone could help me clear things up.
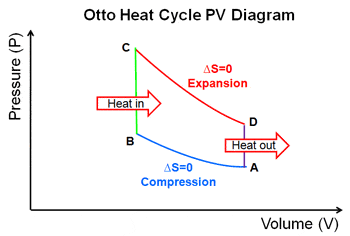
First question, isn't the Otto cycle reversible and usable as a refrigerator? Referring to the diagram above & let me go part by part.
AD: Assume the corresponding part of the working substance is colder than the cold reservoir, heat would flow from the cold reservoir into the working substance, no thermodynamics law broken.
DC: The working substance then undergoes adiabatic/isentropic compression and it temperature rises, no laws forbidding that either.
CB: It then seems possible that the working substance was heated, in the previous step, to a temperature higher than the hot reservoir, and thus heat would flow from the working substance to the hot reservoir.
BA: Adiabatic/isentropic expansion. Similar to DC.
---
Now comes the next question, what makes the Carnot Cycle the most efficient cycle. I've googled 2 explanations for it but still can't understand either.
The 1st explanation is its reversible, or at least as reversible as possible while still able to do work, thus the isothermal processes. However, why does reversibility/equilibrium-ity make it the most efficient. And also from the 1st question, isn't the Otto cycle reversible too?
The 2nd explanation is by contradiction. A super-engine and a Carnot cycle fridge would output work, while the working substance and the system in general is returned to its original state. This breaks the laws and would supposedly prove that the super-engine cannot exist. However, consider a Carnot cycle engine and a less efficient fridge (like say a Otto cycle fridge from the 1st question). The same thing would happen. Does this mean that the super-engine or Carnot cycle engine is fake? Or more likely that the less efficient fridge or Carnot Cycle fridge is not the most efficient.
First question, isn't the Otto cycle reversible and usable as a refrigerator? Referring to the diagram above & let me go part by part.
AD: Assume the corresponding part of the working substance is colder than the cold reservoir, heat would flow from the cold reservoir into the working substance, no thermodynamics law broken.
DC: The working substance then undergoes adiabatic/isentropic compression and it temperature rises, no laws forbidding that either.
CB: It then seems possible that the working substance was heated, in the previous step, to a temperature higher than the hot reservoir, and thus heat would flow from the working substance to the hot reservoir.
BA: Adiabatic/isentropic expansion. Similar to DC.
---
Now comes the next question, what makes the Carnot Cycle the most efficient cycle. I've googled 2 explanations for it but still can't understand either.
The 1st explanation is its reversible, or at least as reversible as possible while still able to do work, thus the isothermal processes. However, why does reversibility/equilibrium-ity make it the most efficient. And also from the 1st question, isn't the Otto cycle reversible too?
The 2nd explanation is by contradiction. A super-engine and a Carnot cycle fridge would output work, while the working substance and the system in general is returned to its original state. This breaks the laws and would supposedly prove that the super-engine cannot exist. However, consider a Carnot cycle engine and a less efficient fridge (like say a Otto cycle fridge from the 1st question). The same thing would happen. Does this mean that the super-engine or Carnot cycle engine is fake? Or more likely that the less efficient fridge or Carnot Cycle fridge is not the most efficient.