You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What Type of Signal is x(t) in Parseval's Theorem?
- Thread starter Jiho
- Start date
AI Thread Summary
In Parseval's Theorem, the signal x(t) can be any complex or real-valued function for which the continuous Fourier transform exists. It is commonly interpreted as representing voltage or current signals, where the theorem relates to the total energy of the signal. The discussion raises concerns about interpreting x(t) as a power signal, questioning how power squared could equate to power due to differing units. The consensus is that while x(t) can technically represent power, this interpretation complicates the usual energy-based understanding of the theorem. Ultimately, the most straightforward application of Parseval's Theorem pertains to voltage or current signals.
Physics news on Phys.org
Delta2
Homework Helper
- 6,002
- 2,628
Mathematically, ##x(t)## can be any function ##x:\mathbb{R}\rightarrow\mathbb{C}## that is any complex valued function over the real line (or as a sub case any real valued function over the real line ##x:\mathbb{R}\rightarrow\mathbb{R}##) for which its continuous Fourier transform ##X(f)## exists . So it can be a function representing the (complex) voltage between two nodes of a circuit or the power between two nodes of a circuit.
However the usual interpretation of this theorem in signal analysis is that the two sides of the equation are just two different ways of computing the total energy of a signal ##x(t)## (a voltage or a current signal).
However the usual interpretation of this theorem in signal analysis is that the two sides of the equation are just two different ways of computing the total energy of a signal ##x(t)## (a voltage or a current signal).
Jiho
- 20
- 4
you mentioned it doesn't matter that signal x(t) represents voltage or power. But I can't understand if x(t) represent power,
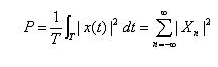 this equation doesn't make sense as I think. In my opinion, How can power^2 be just power?? Unit of dimension is not same as I know.
this equation doesn't make sense as I think. In my opinion, How can power^2 be just power?? Unit of dimension is not same as I know.
Attachments
Delta2
Homework Helper
- 6,002
- 2,628
Yes I said that ##x(t)## can be any function for which the Fourier transform exists. However I also said that the usual interpretation is that of energy (the integrals in both sides represent energy) in the case ##x(t)## is a voltage or current signal. If ##x(t)## is a power signal then we can't give that usual interpretation of energy to this theorem.
(Disclaimer: this is not a HW question. I am self-studying, and this felt like the type of question I've seen in this forum. If there is somewhere better for me to share this doubt, please let me know and I'll transfer it right away.)
I am currently reviewing Chapter 7 of Introduction to QM by Griffiths. I have been stuck for an hour or so trying to understand the last paragraph of this proof (pls check the attached file). It claims that we can express Ψ_{γ}(0) as a linear combination of...
Similar threads
- Replies
- 8
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 9
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 11
- Views
- 880
- Replies
- 7
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 2K
Hot Threads
-
Sequential measurements in quantum mechanics
- Started by hmparticle9
- Replies: 27
- Advanced Physics Homework Help
-
Understanding the double square well potential
- Started by hmparticle9
- Replies: 16
- Advanced Physics Homework Help
-
Trajectory of a particle in polar coordinates
- Started by whatever itis
- Replies: 18
- Advanced Physics Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math