pepediaz
- 49
- 5
- Homework Statement
- Given the lattice shown in attempt to a solution, consider white circles are atoms (of the same type). What would be the Wigner-Seitz cell of this lattice?
- Relevant Equations
- Not actually
I know WS cell only contains one lattice point, so we would have to trace bisectors, and obtain some kind of irregular shape.
Anyways, I wanted to check if what I did is okay. It is considering a fictitious point as the center of the (non-primitive) unit cell, which would be one of those hexagons. I don't know if the dotted square would be a WS, or if I should obtain an irregular shape.
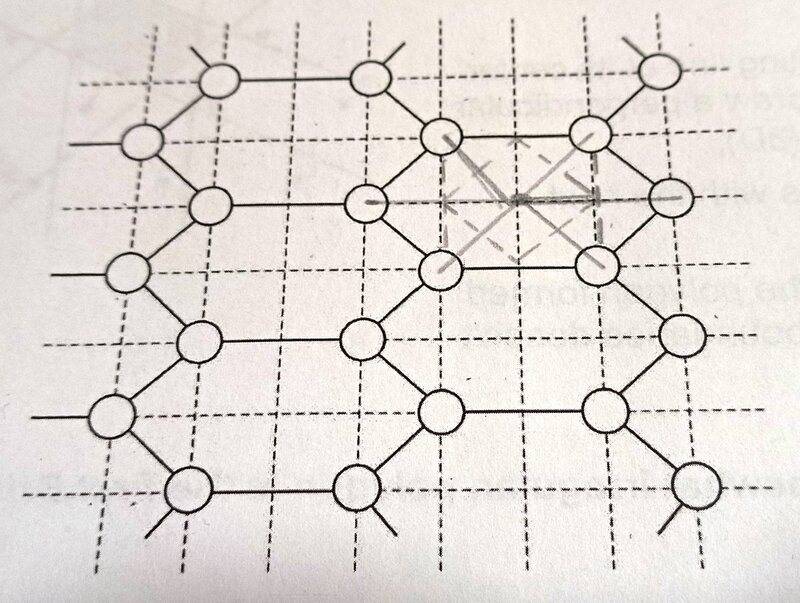
Anyways, I wanted to check if what I did is okay. It is considering a fictitious point as the center of the (non-primitive) unit cell, which would be one of those hexagons. I don't know if the dotted square would be a WS, or if I should obtain an irregular shape.