Where Do the Diagonals of a Parallelogram Intersect?

[evinda]

Hello! (Wave)

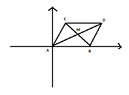
Suppose that a parallelogram $ABCD$ has vertices $A=(0,0)$ and $B=(1,0)$. In terms of $C=(x,y)$, find the position of $D$ and where the two diagonals will intersect.

Then we will have something like that:

View attachment 5378How can we find the coordinates of $M$, i.e. the point at which the two diagonals intersect?

 

[Evgeny.Makarov]

Note that $\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{AD}=2\overrightarrow{AM}$. You should use the connection between the coordinates of points and the coordinates of vectors, as well as rules for operations on vectors in terms of coordinates.

 

[evinda]

Does it hold that $\vec{AD}=2\vec{AM}$ from the fact that each diagonal of a parallelogram separates it into two equal triangles?I found that $D=(x \pm 1, y)$.

Let $M=(\mu_1, \mu_2)$.

So we have $\vec{AD}=(x \pm 1, y)$ and $\vec{AM}=(\mu_1, \mu_2)$.

So $\vec{AD}=2\vec{AM} \Rightarrow x \pm 1= 2 \mu_1 \text{ and } y=2 \mu_2 \Rightarrow \mu_1=\frac{x \pm 1}{2} \text{ and } \mu_2=\frac{y}{2}$

Thus $M=\left( \frac{x \pm 1}{2}, \frac{y}{2} \right)$. Right?

 

[Evgeny.Makarov]

Does it hold that $\vec{AD}=2\vec{AM}$ from the fact that each diagonal of a parallelogram separates it into two equal triangles?

Yes, but it's easier to refer to the known fact that diagonals in a parallelogram are divided in half by the intersection point.

I found that $D=(x \pm 1, y)$.

It should be $D=(x + 1, y)$ because the $x$-coordinate of $B$ is $1$, not $-1$. The rest is correct.

 

[evinda]

Yes, but it's easier to refer to the known fact that diagonals in a parallelogram are divided in half by the intersection point.

Is this known as a theorem?

It should be $D=(x + 1, y)$ because the $x$-coordinate of $B$ is $1$, not $-1$. The rest is correct.

Couldn't we have D=(x-1,y) if we put D at the position I put C at the graph that I have drawn and C at the position of D?
Or am I wrong?

 

[Evgeny.Makarov]

Is this known as a theorem?

Yes.

Couldn't we have D=(x-1,y) if we put D at the position I put C at the graph that I have drawn and C at the position of D?

You are right, it depends on the order of vertices. In fact, calling a quadrangle (and, more generally, a polygon) $XYZW$ usually means that the order of vertices is $X,Y,Z,W$ if they are visited in the counterclockwise or clockwise order. Using this rule, the parallelogram in post #1 should be called $ABDC$.

 

[evinda]

Yes.

Ah, I see... (Nod)

You are right, it depends on the order of vertices. In fact, calling a quadrangle (and, more generally, a polygon) $XYZW$ usually means that the order of vertices is $X,Y,Z,W$ if they are visited in the counterclockwise or clockwise order. Using this rule, the parallelogram in post #1 should be called $ABDC$.

So $X$ has to be connected with $Y$, $Y$ with $Z$, $Z$ with $W$ and $W$ with $X$, right?

I considered the parallelogram ABCD and then I got that $\vec{AC}=2 \vec{AM} \Rightarrow (x,y)=(2 \mu_1, 2 \mu_2)
\Rightarrow \mu_1=\frac{x}{2}$ and $\mu_2=\frac{y}{2}$.

So $M=\left( \frac{x}{2}, \frac{y}{2} \right)$, right?

 

[Evgeny.Makarov]

So $X$ has to be connected with $Y$, $Y$ with $Z$, $Z$ with $W$ and $W$ with $X$, right?

That's how it is usually done.

I considered the parallelogram ABCD and then I got that $\vec{AC}=2 \vec{AM} \Rightarrow (x,y)=(2 \mu_1, 2 \mu_2)
\Rightarrow \mu_1=\frac{x}{2}$ and $\mu_2=\frac{y}{2}$.

So $M=\left( \frac{x}{2}, \frac{y}{2} \right)$, right?

Correct.

 

[evinda]

Great... Thanks a lot! (Smirk)