JohnnyLaws
- 10
- 0
- Homework Statement
- We have a 4-meter-long uniform bar weighing 100 kg, and a person weighing 75 kg is walking across it. The statement specifies a stationary point C situated 2.5 meters away from the origin where the bar can rotate. The question is: 'What distance can this person move away while keeping the bar in equilibrium?'
- Relevant Equations
- I believe that I should set all torques equal to 0 and forces too but I don't know How to draw this specific Free body Diagram. On the other hand I don't know why I need point C.
So here is my equations:
Ra = reaction in A
Rx = reaction in person
Wb = bar's weight
Wp = Person's weight
Forces:
Ra+Rx+Wb+Wp = 0
Ra+Rx-100-75 = 0
Torques:
0*Ra+x*Rx-2*100-x*75 = 0
I think that explained all in "Relevant equations".
Here is the image of this exercise:
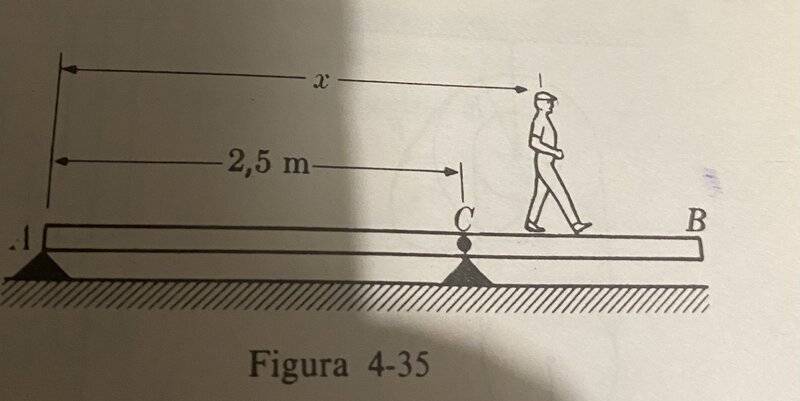
This is my Free Body Diagram:
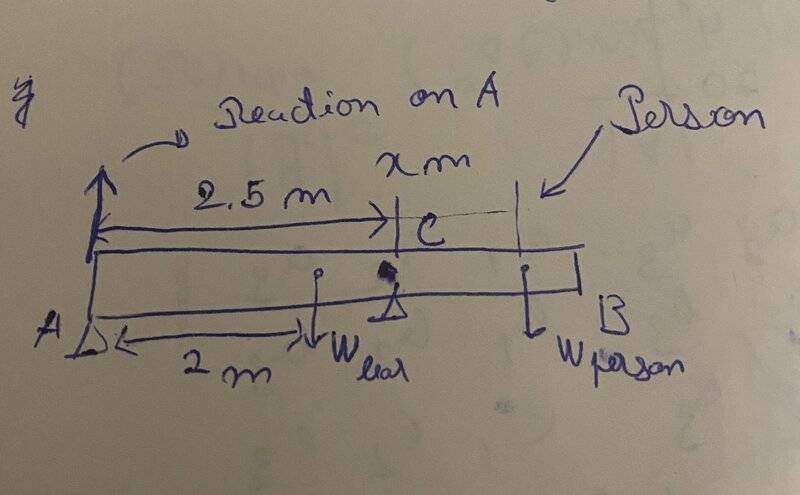
Here is the image of this exercise:
This is my Free Body Diagram:
Last edited by a moderator: