- #1
ymnoklan
- 59
- 3
- Homework Statement
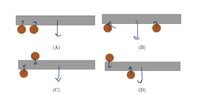
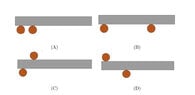
- A rod with a square cross-section is imagined to be supported by two smooth cylinders in four different ways (see figure). Draw all the forces acting on the rod in each case, and use what you know about equilibrium and torque to assess whether it is possible to keep the rod supported in each of these four configurations.
- Relevant Equations
- Sigma F = 0, Sigma tau = 0, tau = F*r*sin(theta), G = m*g
(My attempt of drawing the forces is the figure with the arrows). Intuitively I would say that non of the rods are supported in any of these configurations, but I struggle to give a good explanation for why. I could guess that B would be able to keep up, however summing the forces, it seems just as unbalanced as A (which obviously can’t be supported). What have I misunderstood/overlooked?