- #1
EddiePhys
- 131
- 6
If I have force, or any function f(z), I was told that I can assume it to be constant only in the interval dz.
However, in this case, I had to calculate the work done by the spring force as a function of y
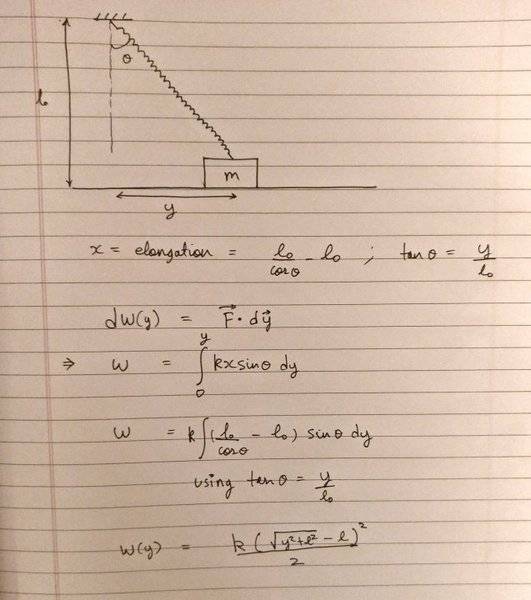
Over here, I assumed the spring force, which is a function of its elongation x (F = -kx) to be constant in the interval dy and integrated and this gave me the correct answer
I want to know why the error vanished over here. Shouldn't spring force only be constant in the interval dx and not dy?
I also want to know, in general, if I have a function, how to decide whether it is constant in some particular interval/in which cases the error will vanish as I take the limit and integrate. Or are forces/functions constant for any infinitesimal intervals such as Rdθ, dy/cosθ, dz etc etc.?
However, in this case, I had to calculate the work done by the spring force as a function of y
Over here, I assumed the spring force, which is a function of its elongation x (F = -kx) to be constant in the interval dy and integrated and this gave me the correct answer
I want to know why the error vanished over here. Shouldn't spring force only be constant in the interval dx and not dy?
I also want to know, in general, if I have a function, how to decide whether it is constant in some particular interval/in which cases the error will vanish as I take the limit and integrate. Or are forces/functions constant for any infinitesimal intervals such as Rdθ, dy/cosθ, dz etc etc.?