Why can't Solar panels be hemispherical, or a curved strip type?

[Aashna4M]

TL;DR Summary

wont a curved surface have more area exposed to sunlight while simultaneously occupying less land space

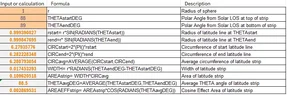
comparing a flat solar panel of area 2π r² and a hemisphere of the same area, the hemispherical solar panel would only occupy the area π r² of while the flat panel would occupy an entire 2π r² of land. wouldn't the hemispherical version have the same area of panel exposed to the sun, occupy less land space and can therefore increase the number of panels one land can have fitted? this would increase the power output proportionally as well.
when I searched it up I wasn't satisfied with the answer that came up- that the entire panel would not be lit. In my argument, the entire hemisphere can be lit and it can also generate electricity from the sunlight for a longer duration of the day too? if the lateral sides of the hemisphere are an issue, why not a curved strip?

 

[phinds]

Have you given any consideration to the effectiveness of highly angled sunlight on a panel?

 

[DaveE]

Solyndra tried something like that. It didn't work out very well for them. Solar panels need to be cheap. Flat is cheap to make and easy to install.

 

[Aashna4M]

Have you given any consideration to the effectiveness of highly angled sunlight on a panel?

wouldn't the same issue persist with the flat panels too?

 

[Aashna4M]

Solyndra tried something like that. It didn't work out very well for them. Solar panels need to be cheap. Flat is cheap to make and easy to install.

financial aspect yes i guess

 

[jbriggs444]

comparing a flat solar panel of area 2π r² and a hemisphere of the same area, the hemispherical solar panel would only occupy the area π r² of while the flat panel would occupy an entire 2π r² of land. wouldn't the hemispherical version have the same area of panel exposed to the sun,

Let me make sure I understand the comparison.

On the one hand we have a disc shaped flat solar panel with area $2\pi r^2$. So the radius of the disc must be about $1.4 r$. It is sitting flat on the ground.

On the other hand we have a hemispherical solar panel sitting flat on the ground with the domed side up. It has a surface area of $2\pi r^2$ as well. So the radius of the hemisphere must be $r$.

You ask whether the amount of sun intercepted by both would be the same.

If the sun is directly overhead then the disc will intercept twice as much sun as the hemisphere.

If the sun is angled (and if the collectors are not angled to match) then the ratio would not be two to one. The hemisphere would intercept sunlight from the side. And consequently shade adjacent areas.

There is no advantage to be gained in this manner. It is not surface area that counts. It is cross-sectional area on a plane facing the sun that is relevant.