laprec
- 18
- 0
Given that √5 tanA=-2 and CosB=8/17 in ∆ABC
State why we may assume that angle C is acute and determine the value of Sin CAttempt made:
tanA=-2/√5 CosB=8/17
A is obtuse angle of 138° or reflex angle 318.19°
B is an acute angle of61.9° or reflex angle298.1 °.Since it is a right triangle,therefore angle C is acute
Not sure the above is correct though!
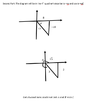
Second Part: The diagram will be in the 4th quadrant since tan is negative and cos is positive
State why we may assume that angle C is acute and determine the value of Sin CAttempt made:
tanA=-2/√5 CosB=8/17
A is obtuse angle of 138° or reflex angle 318.19°
B is an acute angle of61.9° or reflex angle298.1 °.Since it is a right triangle,therefore angle C is acute
Not sure the above is correct though!
Second Part: The diagram will be in the 4th quadrant since tan is negative and cos is positive
Attachments
Last edited: