Mike_bb
- 191
- 19
- TL;DR
- Why is Delta y not equal to dy for infinitesimally dx on the graph?
Hello!
As is known, \Delta y = dy for infinitesimally small dx. It's true.
But if we have graph we may see that \Delta y isn't equal to dy even for infinitesimally small dx. Why is that so?
Thanks!
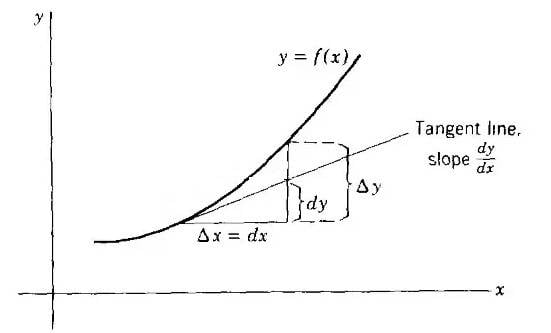
As is known, \Delta y = dy for infinitesimally small dx. It's true.
But if we have graph we may see that \Delta y isn't equal to dy even for infinitesimally small dx. Why is that so?
Thanks!
Last edited: