Working model to demonstrate Lagrange points L4 & L5 -- possible?

[Swamp Thing]

If we fabricate a surface like this...

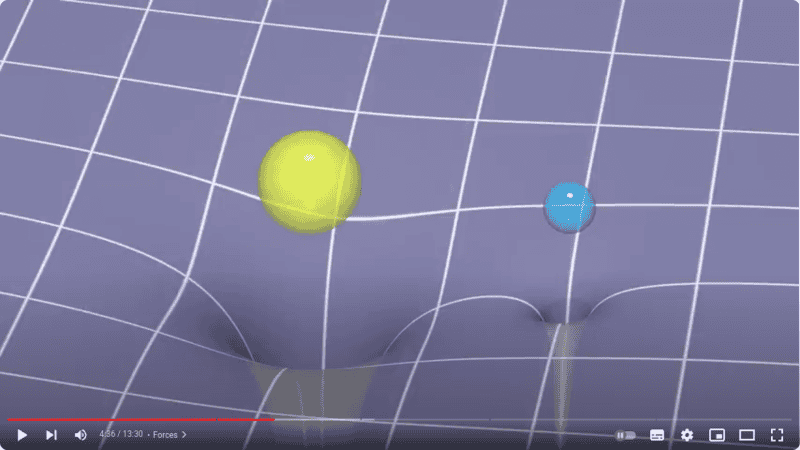
(source:www.youtube.com/watch?v=7PHvDj4TDfM)

... and rotate it around the appropriate vertical axis at the appropriate speed, would it be possible to get a bead to roll in an "orbit" around L4 or L5.

(a) Possible at all in principle?

(b) Practical challenges?

 

[vanhees71]

What should this be good for? We have a well-working model, Newtonian mechanics. See, e.g.,

https://www.mat.univie.ac.at/~westra/lagrangepoints.pdf

 

[Swamp Thing]

At the moment I am not able to access that site -- "network error". (All other usual sites are accessible)
I will try later.

 

[Cutter Ketch]

I see no reason it couldn’t work in principle, but I think it may be too difficult in practical terms.

Even for large museum quality rigid gravity demonstrations friction is pretty high and the orbits decay quickly. You’d have to make it as smooth as possible.

Spinning it on a turntable will introduce vibration that will also decay the orbits. You’d need good bearings.

Another issue would be getting the shape of the gravity wells just right. I don’t know how you would precisely manufacture the double well surface.

You’d have to experiment with the turntable speed, but you should be able to calculate a speed that gives the best Lagrange points. The turntable speed would need to have precise controls

 

[Swamp Thing]

I just found this video that is a bit similar in concept, and it seems to work pretty robustly...



That said, the L4 - L5 problem is much more complex since it involves more things that you have to get just right.

And I found this video which leads to believe that gyroscopic effects in the rolling ball would probably change the behavior in a drastic way and break everything.



Or maybe if one is lucky, the gyroscopic effect may actually make it work better than it would otherwise.