Micko
- 43
- 0
Hello to all,
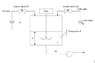
I want to analyze and make model of the water mixing process as shown in file in attacment. Basically, there are two input variables: input hot water flow and cold water flow. There is constant flow FL3. I need to write equation that describe how level and tank's temperature is changing. Equation for the level is:
dh/dt=(FL1(t)+FL2(t)-FL3(t))/Area;
And I need to figure out what equation to use to describe temperature.
At first I thought that this is correct equation:
V*dT/dt = Fl1*T1+Fl2*T2-(FL1+FL2)*T
But I have saw different equation:
V*dT/dt = Fl1*T1+Fl2*T2-FL3*T
Which of these is correct?
I know that these equations should be derived from heat equations m*C*(Ta-Tb), but not sure how to do this.
Can you help?
I want to analyze and make model of the water mixing process as shown in file in attacment. Basically, there are two input variables: input hot water flow and cold water flow. There is constant flow FL3. I need to write equation that describe how level and tank's temperature is changing. Equation for the level is:
dh/dt=(FL1(t)+FL2(t)-FL3(t))/Area;
And I need to figure out what equation to use to describe temperature.
At first I thought that this is correct equation:
V*dT/dt = Fl1*T1+Fl2*T2-(FL1+FL2)*T
But I have saw different equation:
V*dT/dt = Fl1*T1+Fl2*T2-FL3*T
Which of these is correct?
I know that these equations should be derived from heat equations m*C*(Ta-Tb), but not sure how to do this.
Can you help?