- #1
Q-reeus
- 1,115
- 3
In GR normal stresses as per the three lower diagonal terms T11, T22, T33 in the SET (stress-energy tensor) (e.g. http://en.wikipedia.org/wiki/Stress–energy_tensor) are source terms for gravitating mass. And afaik true for any similar theories of gravity. Owing to their being resolved into equal and oppositely signed normal stresses, the off-diagonal shear stress components cannot even formally be a source of gravitation in solids and so are of no relevance here. Elastic/hydrostatic energy with typically quadratic dependence on stress/pressure is formally part of the T00 rest-energy term, and that role for stress is not in doubt.
My contention is that if normal stresses truly are a source for gravitating mass m, it implies the following:
[1] Existence of monopole GW's, which represents an internal inconsistency in GR.
[2] Generation of GW's violating the conservation of energy in general.
First, a situation illustrating [1]
Komar mass is considered a valid definition of gravitating mass m in a stationary metric setting. From Wikipedia article at http://en.wikipedia.org/wiki/Komar_mass#Komar_mass_as_volume_integral_-_general_stationary_metric
With these coordinate choices, we can write our Komar integral as
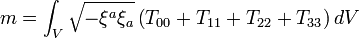
...Essentially, both energy and pressure contribute to the Komar mass. Furthermore, the contribution of local energy and mass to the system mass is multiplied by the local "red shift" factor
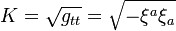
Evidently m above applies for any matter distribution assumed non-rotating and having a stationary center of energy. Apply that to the case of a perfectly elastic thin spherical shell vibrating at natural frequency f in the n = 0 'fundamental' membrane breathing mode (uniform sinusoidal oscillation in radius R). Spherical symmetry allows no mass dipole or quadrupole moments P, Q. Periodic exchange at frequency 2f between KE of radial motion and elastic energy in circumferential uniform biaxial stress/strain leaves total energy (integration over the T00 term) time invariant. [Assuming for the moment a possible tiny monopole GW drain is entirely absent!] The off-diagonal SET shear terms play no role in determining m. For the momentum-energy flux terms Ti0 = -T0i, having radial acting velocity vector character, spherical symmetry implies net cancellation. Even for other configurations such as a straight bar vibrating freely in fundamental axial mode, these 'magnetic' terms, although then non-zero, scale very differently as functions of say material elesticity and density to that for the stress terms considered below.
Which just leaves the Tii stress terms, that are not time invariant. At minimum radial excursion there is positive (compressive) circumferential stress, and negative (tensile) stress at maximum excursion. For the biaxially stressed shell, let's say we have |T11|max = |T22|max = p0 (c=1), with radial component |T33| negligible. Choose time t = 0 when R is undergoing maximum inward motion. If the shell has a thickness δ << R there will be a harmonic monopole moment ms = 4∏R2δp0sin(2∏ft), owing solely to the almost purely biaxial stress. Implying radial acting monopole GW radiation owing to d/dt(ms) = 8∏2R2δp0fcos(2∏ft). (see e.g. http://www.tapir.caltech.edu/~teviet/Waves/gwave.html - with the g' monopole series there continued to 1/r radiative term). [Note that adding in a non-negligible radial T33 contribution (thick shell case not considered) merely acts to redistribute the stress contributions in the Komar expression. All that matters is that pressure is the sole time varying net contribution to m] Contrary to the GR claim that the lowest possible GW mode is pure transverse quadrupolar. As to whether monopole GW generation is a conservative process here requires detailed calculations. It does seem to scale correctly wrt the relevant parameters. Not so for the next example involving forced vibrations.
Now, a situation illustrating [2], first introduced here: https://www.physicsforums.com/showpost.php?p=3790816&postcount=65 , necessarily cleaned up below:
Suppose two 'G'-clamps are welded back-to-back, and by means of say electric motors & batteries, the screws are periodically tightened and loosened. In this forced oscillation regime, frequency assumed well below mechanical self-resonance, inertial forces play no important role. By inspection periodic stresses in the assembly having a quadrupolar type distribution Qs arise - compression in the screwed arms coinciding with tension in the opposite arms, and vice versa. If the screwed legs are taken as verticallly inclined, the stress moment Qs would be linear and horizontal in orientation. Bending and shear stresses also present are self-cancelling wrt net pressure. This dominantly quadrupolar stress distribution acts as a source of quadrupolar GW's whose amplitude for a given driving frequency is directly proportional to the stresses (as Tii source terms for m).
We have not so far included the usual contributions:
a) Gross matter motion under mechanical strain. This is expected to be overwhelmingly the dominant source of GW's. One also expects dominantly vertical strain motion, generating a net vertical linear quadrupole moment Qm, orthogonal to that for stress generated Qs. Hence little if any cross-coupling between the two. Further striking differences between Qm and Qs is the scaling wrt elastic constant E (Young's modulus), and material density ρ. Given a specified driving stress amplitude, strain is inversely proportional to E. Hence gross matter motion and thus Qm scales accordingly. Additionally, Qm is directly proportional to material density ρ. As Qs is in this setting independent of both E and ρ, it is not possible for cross-coupling between these two GW sources to cancel anything in general.
b) Relativistic energy-momentum flux owing to redistributions of energy between the driving power source (battery etc.) and elastic strain energy in the clamps. Suppose this gives rise to a quadrupole moment Qe. The same scaling feature wrt E mentioned above applies here also. As well, by careful arrangement of power sources one could eliminate any quadrupole moment term Qe, leaving only insignificant higher-order terms.
It is this independence from E and ρ of stress contribution Qs to GW amplitude, in this forced oscillation regime, that is critical. Plastic will flex far more than say steel. It follows back reaction from stress generated GW's must induce far greater power drain in the plastic clamps case than for the steel ones. Much longer 'stroke' for the same retarding 'force'. And given the E and ρ parameter dependence of all non-stress GW contributions, there is no way they can in general nullify the conclusion GW's owing to Qs trend to 'for free' as E trends upward. There cannot be in general a conservative power balance. And importantly, this setting is in arbitrarily flat background metric - so Noether's theorem appears to be in serious trouble!
Of course as hinted in the title there is one possible ready cure for all this - pressure is in fact *not* a source of gravity. Assuming no fatal blunders in the foregoing, seems to me a stark choice has to be made. Has pressure as source ever been derived from first principles - as in direct calculation of motion contributed gravitating mass generated by a 'gas' of colliding particles? That might prove to be interesting. If anyone knows of such a study, please provide a reference to the literature. Why was stress inserted into the SET in the first place? Symmetry considerations perhaps - all the SET slots have to mean something physical? My suspicion as complete GR outsider is it was a carry over from SR, where pressure applied to a flowing fluid does exhibit inertial properties as a consequence of non-simultaneity. I believe it can be shown this inertial behaviour, implying a sort of 'mass' to pressure, is really a type of pseudo quantity that fails when stretched just a bit, but this is not the place to expand on that.
Don't expect all this to be taken lying down, so await breathlessly for sensible and constructive critiques.
My contention is that if normal stresses truly are a source for gravitating mass m, it implies the following:
[1] Existence of monopole GW's, which represents an internal inconsistency in GR.
[2] Generation of GW's violating the conservation of energy in general.
First, a situation illustrating [1]
Komar mass is considered a valid definition of gravitating mass m in a stationary metric setting. From Wikipedia article at http://en.wikipedia.org/wiki/Komar_mass#Komar_mass_as_volume_integral_-_general_stationary_metric
With these coordinate choices, we can write our Komar integral as
...Essentially, both energy and pressure contribute to the Komar mass. Furthermore, the contribution of local energy and mass to the system mass is multiplied by the local "red shift" factor
Evidently m above applies for any matter distribution assumed non-rotating and having a stationary center of energy. Apply that to the case of a perfectly elastic thin spherical shell vibrating at natural frequency f in the n = 0 'fundamental' membrane breathing mode (uniform sinusoidal oscillation in radius R). Spherical symmetry allows no mass dipole or quadrupole moments P, Q. Periodic exchange at frequency 2f between KE of radial motion and elastic energy in circumferential uniform biaxial stress/strain leaves total energy (integration over the T00 term) time invariant. [Assuming for the moment a possible tiny monopole GW drain is entirely absent!] The off-diagonal SET shear terms play no role in determining m. For the momentum-energy flux terms Ti0 = -T0i, having radial acting velocity vector character, spherical symmetry implies net cancellation. Even for other configurations such as a straight bar vibrating freely in fundamental axial mode, these 'magnetic' terms, although then non-zero, scale very differently as functions of say material elesticity and density to that for the stress terms considered below.
Which just leaves the Tii stress terms, that are not time invariant. At minimum radial excursion there is positive (compressive) circumferential stress, and negative (tensile) stress at maximum excursion. For the biaxially stressed shell, let's say we have |T11|max = |T22|max = p0 (c=1), with radial component |T33| negligible. Choose time t = 0 when R is undergoing maximum inward motion. If the shell has a thickness δ << R there will be a harmonic monopole moment ms = 4∏R2δp0sin(2∏ft), owing solely to the almost purely biaxial stress. Implying radial acting monopole GW radiation owing to d/dt(ms) = 8∏2R2δp0fcos(2∏ft). (see e.g. http://www.tapir.caltech.edu/~teviet/Waves/gwave.html - with the g' monopole series there continued to 1/r radiative term). [Note that adding in a non-negligible radial T33 contribution (thick shell case not considered) merely acts to redistribute the stress contributions in the Komar expression. All that matters is that pressure is the sole time varying net contribution to m] Contrary to the GR claim that the lowest possible GW mode is pure transverse quadrupolar. As to whether monopole GW generation is a conservative process here requires detailed calculations. It does seem to scale correctly wrt the relevant parameters. Not so for the next example involving forced vibrations.
Now, a situation illustrating [2], first introduced here: https://www.physicsforums.com/showpost.php?p=3790816&postcount=65 , necessarily cleaned up below:
Suppose two 'G'-clamps are welded back-to-back, and by means of say electric motors & batteries, the screws are periodically tightened and loosened. In this forced oscillation regime, frequency assumed well below mechanical self-resonance, inertial forces play no important role. By inspection periodic stresses in the assembly having a quadrupolar type distribution Qs arise - compression in the screwed arms coinciding with tension in the opposite arms, and vice versa. If the screwed legs are taken as verticallly inclined, the stress moment Qs would be linear and horizontal in orientation. Bending and shear stresses also present are self-cancelling wrt net pressure. This dominantly quadrupolar stress distribution acts as a source of quadrupolar GW's whose amplitude for a given driving frequency is directly proportional to the stresses (as Tii source terms for m).
We have not so far included the usual contributions:
a) Gross matter motion under mechanical strain. This is expected to be overwhelmingly the dominant source of GW's. One also expects dominantly vertical strain motion, generating a net vertical linear quadrupole moment Qm, orthogonal to that for stress generated Qs. Hence little if any cross-coupling between the two. Further striking differences between Qm and Qs is the scaling wrt elastic constant E (Young's modulus), and material density ρ. Given a specified driving stress amplitude, strain is inversely proportional to E. Hence gross matter motion and thus Qm scales accordingly. Additionally, Qm is directly proportional to material density ρ. As Qs is in this setting independent of both E and ρ, it is not possible for cross-coupling between these two GW sources to cancel anything in general.
b) Relativistic energy-momentum flux owing to redistributions of energy between the driving power source (battery etc.) and elastic strain energy in the clamps. Suppose this gives rise to a quadrupole moment Qe. The same scaling feature wrt E mentioned above applies here also. As well, by careful arrangement of power sources one could eliminate any quadrupole moment term Qe, leaving only insignificant higher-order terms.
It is this independence from E and ρ of stress contribution Qs to GW amplitude, in this forced oscillation regime, that is critical. Plastic will flex far more than say steel. It follows back reaction from stress generated GW's must induce far greater power drain in the plastic clamps case than for the steel ones. Much longer 'stroke' for the same retarding 'force'. And given the E and ρ parameter dependence of all non-stress GW contributions, there is no way they can in general nullify the conclusion GW's owing to Qs trend to 'for free' as E trends upward. There cannot be in general a conservative power balance. And importantly, this setting is in arbitrarily flat background metric - so Noether's theorem appears to be in serious trouble!
Of course as hinted in the title there is one possible ready cure for all this - pressure is in fact *not* a source of gravity. Assuming no fatal blunders in the foregoing, seems to me a stark choice has to be made. Has pressure as source ever been derived from first principles - as in direct calculation of motion contributed gravitating mass generated by a 'gas' of colliding particles? That might prove to be interesting. If anyone knows of such a study, please provide a reference to the literature. Why was stress inserted into the SET in the first place? Symmetry considerations perhaps - all the SET slots have to mean something physical? My suspicion as complete GR outsider is it was a carry over from SR, where pressure applied to a flowing fluid does exhibit inertial properties as a consequence of non-simultaneity. I believe it can be shown this inertial behaviour, implying a sort of 'mass' to pressure, is really a type of pseudo quantity that fails when stretched just a bit, but this is not the place to expand on that.
Don't expect all this to be taken lying down, so await breathlessly for sensible and constructive critiques.
Last edited: