Conditional probability Definition and 242 Threads

In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. If the event of interest is A and the event B is known or assumed to have occurred, "the conditional probability of A given B", or "the probability of A under the condition B", is usually written as P(A|B), or sometimes PB(A) or P(A/B). For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell is coughing might be 75%, in which case we would have that P(Cough) = 5% and P(Cough|Sick) = 75%.
Conditional probability is one of the most important and fundamental concepts in probability theory. But conditional probabilities can be quite slippery and might require careful interpretation. For example, there need not be a causal relationship between A and B, and they don't have to occur simultaneously.
P(A|B) may or may not be equal to P(A) (the unconditional probability of A). If P(A|B) = P(A), then events A and B are said to be independent: in such a case, knowledge about either event does not alter the likelihood of each other. P(A|B) (the conditional probability of A given B) typically differs from P(B|A). For example, if a person has dengue, they might have a 90% chance of testing positive for dengue. In this case, what is being measured is that if event B ("having dengue") has occurred, the probability of A (test is positive) given that B (having dengue) occurred is 90%: that is, P(A|B) = 90%. Alternatively, if a person tests positive for dengue, they may have only a 15% chance of actually having this rare disease, because the false positive rate for the test may be high. In this case, what is being measured is the probability of the event B (having dengue) given that the event A (test is positive) has occurred: P(B|A) = 15%. Falsely equating the two probabilities can lead to various errors of reasoning such as the base rate fallacy. Conditional probabilities can be reversed using Bayes' theorem.
Conditional probabilities can be displayed in a conditional probability table.

View More On Wikipedia.org
Recent contents Top users
  1. Hamiltonian

    Finding a conditional probability from joint p.d.f

    using the equation mentioned under Relevant Equations I can get, $$\mathbb{P}(2X > Y |1 < 4Z < 3) = \frac{\mathbb{P}(2X>Y, 1<4z<3)}{\mathbb{P}(1<4z<3)}$$ I can find the denominator by finding the marginal probability distribution, ##f_{Z}(z)## and then integrating that with bounds 0 to 1. But I...
  2. WMDhamnekar

    Stochastic Calculus: Conditional Expectation

  3. MathMan2022

    Conditional probability problem

    A) P(A and B) = 0.45 * 5/10 B P(Not B) = 1 - ( 0.45 * 5/10) Is it like this?
  4. V

    Expected Value of Election Results

    I submitted this solution, and it was marked incorrect. Could I get some feedback on where I went wrong? Let S represent the event that Party A wins the senate and H represent the event that Party A wins the house. There are 4 cases: winning the senate and house (##S \cap H##), winning just...
  5. WMDhamnekar

    MHB What Is the Probability of Distributing Remaining Trump Cards in Bridge?

    North and south have ten trumps between them ( trumps being cards of specified suit). (a) Find the probability that all three remaining trumps are in the same hand. (that is either east or west has no trumps). (b) If it is known that king of trumps is included among the three, what is the...
  6. C

    I Taking socks out of drawers, conditional probability

    Problem: In a dresser there are 3 drawers. In one drawer there are two black socks and one white sock, in the second drawer there are two white socks, and in the third drawer there is a black and white sock. Suppose I chose a drawer randomly ( meaning, in a uniform distribution ) and I took a...
  7. S

    Conditional probability of a test records this positive result

    My attempt: $$P(\text{B is positive}|\text{A is positive})=\frac{P(\text{B is positive} \cap \text{A is positive})}{P(\text{A is positive})}$$ $$=\frac{P(\text{B is positive})\times P(\text{A is positive})}{P(\text{A is positive})}$$ $$=P(\text{B is positive})$$ $$=0.01 \times 0.99 + 0.99 \times...
  8. P

    B Decision for conditional probability instead of intersection of events

    Hello, I have a question about the following sentence and would appreciate if someone could explain how to read out the conditional probability here. "Each microwave produced at factory A is defective with probability 0.05". I understand the sentence as the intersection ##P(Defect \cap...
  9. Moara

    Conditional probability and criminal DNA analysis

    We know that ##P(A-) = (95\% \cdot 0.5\% + 5\% \cdot 98.5\% )## and ##P(guilty \ and \ A-) = (95\% \cdot 0.5\%)##, so letter a) is just ##P(guilty \ and \ A-)/P(A-)##. What I tried to do in letter b) was again using the conditional probability theorem. First calculating the probability that...
  10. Moara

    Observation of events and analysis of the associated Hypotheses

    For letter a), i think that he is assuming that each hypothesis is independent, and that they are mutually exclusive.For letter b), I understand that it indeed admits the relative frequency interpretation, since the the experiment is being produced several times. For letter c) we do the...
  11. chwala

    Solve the conditional probability question

    My question is on part ##c## of the problem. Kindly see attached question,...is the second approach correct?
  12. M

    Probability notation: question about joint and conditional probability

    Hi, Just a quick question about conditional and marginal probabilities notation. Question: What does ## p(a|b, c) ## mean? Does it mean: 1) The probability of A, given (B and C) - i.e. ## p[A | (B \cap C)] ## OR 2) The probability of (A given B) and C - i.e. ## p[(A | B) \cap C] ## I was...
  13. jisbon

    Conditional Probability + Poisson Distribution

    Confused and not sure if it is correct, but please do correct my steps. We let event B be that there are at least 3 customers entering in 5 minutes. Hence P(B) = 1- P(X=0)- P(X=1) - P(X=2) = ##1- \dfrac{e^{-5}5^{0}}{0!}-\dfrac{e^{-5}5^{1}}{1!}-\dfrac{e^{-5}5^{2}}{2!} ## = 0.8753... Now we let...
  14. Addez123

    Conditional probability of dying from eating a poison fruit

    Summary:: There's 11 fruits, 3 of which is poisionous. A guy eats 4 of them, a girl eats 6 and a dog gets the last one. What is the conditional probability of both the girl and guy dying IF the dog made it? One fruit is enough to kill you. $$P(dog lives) = 8/11$$ $$P(allPeopleDie | dog...
  15. CaptainX

    B What is Conditional Probability and its Properties?

    1. Definition If E and F are two events associated with the same sample space of a random experment, the conditional probability of the event E given that F has occurred, i.e. P(E|F) is given by P(E|F) = (E∩F)/P(F) (P≠0) 2. Properties of conditional probability Let E and F be events of...
  16. Manasan3010

    Is an answer possible - Conditional Probability

    I am a noob to this topic so correct me If I made any silly mistake. By plugging in the values I managed to get p(abc)=0.75*0.9*p(c|ab) Here How can I find p(c|ab)? Is this question unsolvable or can I derive it? I also want to know what is meant by p(abc) in literary terms. I also created a...
  17. Calculuser

    I A Lottery Game With Conditional Probability?

    Question: "In a lottery game each player tries to guess right 6 numbers designated in advance by choosing randomly from among numbers from 1 to 20. Given that one player guessed right 5 numbers out of 6 that he/she picked, what is the probability of guessing right the 6 numbers?" The problem...
  18. Eclair_de_XII

    How do I derive this expression for conditional probability?

    ##P(T=1|W=w)=\frac{P(\{T=1\}\cap\{W=w\})}{P(W=w)}=\frac{\binom {n-2} {w-1} p^{w-1}(1-p)^{(n-2)-(w-1)}}{\binom n w p^w (1-p)^{n-w}}=\frac{(n-2)!}{(w-1)!(n-w-1)!}\frac{w!(n-w)!}{n!}\frac{1}{p(1-p)}=\frac{w(n-w)}{n(n-1)}(p(1-p))^{-1}##. I cannot seem to get the terms with ##p## out of my expression.
  19. C

    MHB Calculating Conditional Probability of Male/Female Customers Buying Books A-D

    There are 4 books being sold in the bookshop : A, B, C, D. We know that 20% of the male customers buy book A at least once a week, 55% buy book B at least once a week, 25% buy book C at least once a week and 15% buy book D at least once in a month. We also know that 32% of the female customers...
  20. H

    Conditional Probability of a continuous joint distribution function

    For 1) I found two ways but I get difference results. The first way is I use P(A|B) = P(A and B)/P(B). I get P(X<1|Y<1)=(∫_0^1▒∫_0^1▒〖3/4 (2-x-y)dydx〗)/(∫_0^1▒∫_0^1▒〖3/4 (2-x-y)dydx〗+∫_1^2▒∫_0^(2-x)▒〖3/4 (2-x-y)dydx〗)=6/7 The 2nd method is I use is f(x│y)=f(x,y)/(f_X (x)...
  21. Vital

    I Getting to Grips with Bayes' Formula: Exploring the Problem & Questions

    Hello! I am trying to get to grips with the Bayes' formula by developing an intuition about the formula itself, and on how to use it, and how to interpret. Please, take a problem, and my questions written within them - I will highlight my questions and will post them as I add the information...
  22. Vital

    I Conditional probability choosing from the objects

    Hello. I am reading an online stats book, and there is the following question, which I solved incorrectly, and I think I understand what is my mistake, but I will be grateful for your explanation, if I have incorrectly detected the logic behind my mistake. I am weak at math (trying to improve it...
  23. N

    MHB Conditional Probability and Venn Diagrams

    I am having a hard time with the following exercise: Assume for this problem that the company has 8 Chevrolets and 4 Jeeps, and two cars are selected randomly and given to sales representatives. What is the probability of both cars being Chevrolets, given that both are of the same make? I...
  24. N

    MHB Help with Math Homework: Conditional Probability - 19/30

    Hey! I need help with my Math homework :( The question is the following... There are 5 history courses of interest to Howard, including 3 in the afternoon, and there are 6 psychology courses, including 4 in the afternoon. Howard picks a course by selecting a dept at random, then selecting a...
  25. D

    Conditional probability reasoning problem

    Homework Statement Out of all the products a company makes 2% is damaged. During the routine control of the products, the products are put to a test which discovers the damaged ones in 99% of the cases. In 1% however it approves the damaged item as a working one and vice versa. Find the...
  26. L

    Basic probability, conditional probability

    Homework Statement what is the probability that a component which is still working after 800 hrs, will last for at least 900hrs Homework Equations conditional probability P(E|A) = ( P( E ∩ A) ) / ( P(A) ) The Attempt at a SolutionIm just checking my own understanding if this problem is...
  27. R

    Bayesian Probability Distributions

    Hi, I was having some trouble doing some bayesian probability problems and was wondering if I could get any help. I think I was able to get the first two but am confused on the last. If someone could please check my work to make sure I am correct and help me on the last question that would be...
  28. M

    MHB Conditional Probability with 3 Events

    I'm currently stuck on a question that involves conditional probability with 3 events. This is a concept that I'm having the most trouble grasping and trying to solve in this subject. I am not sure how to start this problem. The Question: Given that P(A n B) = 0.4, P(A n C) = 0.2, P(B|A)=0.6...
  29. Avatrin

    I Equality in conditional probability

    Hi In Dudas Pattern Classification, he Writes that P(x,\theta|D) can always be written as P(x|\theta,D)P(\theta|D) . However, I cannot find any justification for this. So, why are these Equal?
  30. G

    I Rewriting of equality in conditional probability distribution

    I don't get $$\frac{P[x<X<x+dx|N=n]}{dx}=f_{X|N}(x|n)$$ Can someone derive why? I would believe that $$f_{X|N}(x|n)=\frac{f(x,N)}{p_n(N)}$$ but I don't get how that would be the same. And I don't get that $$\frac{P[x<X<x+dx|N=n]}{dx}=\frac{P[N=n|x<X<x+dx]}{P[N=n]}\frac{P[x<X<x+dx]}{dx}$$ Can...
  31. Clifford Engle Wirt

    B Conditional Probability, Independence, and Dependence

    (Mentor note: link removed as not essential to the question.) The problem is: what is relevance anyhow? My questions are these: did I get the math right in the following? Is there a better, more acceptable way to lay out the sample space Ω and the two events F and E? Apart from the math...
  32. S

    B Loophole on theorem related to Conditional Probability

    The theorem says The probability that an event B occur after A has already occurred is given by P(B/A) =P(A intersection B) /P(A) But applying thus to a problem like the probability of occurrence of all 3 tails on 3 coins when tossed if 1 tail has already occurred is P(B/A) =(1/8)/(7/8)=1/7...
  33. N

    MHB Conditional Probability - Faulty Plumbing

    This question has been driving me crazy. A large industrial firm uses three local motels to provide overnight accommodations for its clients. From past experience it is known that 20% of the clients are assigned rooms at the Ramada Inn, 50% at the Sheraton and 30% at Lakeview. What is the...
  34. M

    MHB Conditional probability prove or disprove

    Hey! :o Let $P$ be a probability measure on a $\sigma$-Algebra $\mathcal{A}$. I want to prove or disprove the following statements: $P(A\mid B)=1-P(\overline{A}\mid B)$, for $A, B\in \mathcal{A}$ $P(A\mid B)=1-P(A\mid \overline{B})$, for $A, B\in \mathcal{A}$ I have done the following...
  35. J

    B What Is the Probability of Scoring in the 88th Percentile for a Trait as a Male?

    I scored in the 88th percentile in a certain personality trait and am trying to figure out the probability of that given that I'm male. I'm trying the likelihood that I would land in the 88th percentile given that I'm male. Definitions: T = trait, M = males, F = female. Given: P(T|M) = 0.3...
  36. A

    I Question: Proposed Solution to Two Envelope Paradox

    Su, Francis, et. al. have a short description of the paradox here: https://www.math.hmc.edu/funfacts/ffiles/20001.6-8.shtmlI used that link because it concisely sets forth the paradox both in the basic setting but also given the version where the two envelopes contain ( \,\$2^k, \$2^{k+1}) \...
  37. R

    MHB What Is the Probability Distribution for Drawing Spades Without Replacement?

    Dear All sorry for repeated post; There is a problem Problem: Three cards are drawn in succession from a deck without replacement. find the probability distribution for the number of spades. I have come with this solution. Let S1: appearance of spade on first draw S2: appearance of spade on 2nd...
  38. R

    MHB Calculating the Probability of Faulty Plumbing in Hotel Rooms: A Case Study

    Dear all Please help in solving the following problem. A large industrial firm uses 3 local motels to provide overnight accommodations for its clients. from past experience, it is known that 20% of the clients are assigned rooms at the Ramada Inn, 50% at the sheeraton and 30% at the Lakeview...
  39. W

    I Poisson distribution with conditional probability

    Hi guys, I have a question about computing conditional probabilities of a Poisson distribution. Say we have a Poisson distribution P(X = x) = e^(−λ)(λx)/(x!) where X is some event. My question is how would we compute P(X > x1 | X > x2), or more specifically P(X> x1 ∩ X > x2) with x1 > x2? I...
  40. HaLAA

    Conditional Probability and law of total probability

    Homework Statement It rains in a city with a chance of 0.4. The weather forecast is not always accurate. When there will be a rain the next day, the forecast predicts the rain with probability 0.8; When there is no rain, the forecast falsely predicts a rain with probability 0.1. You take your...
  41. J

    MHB What is the probability of a customer only insuring one non-sports car?

    Need help with a probability problem. I have the answer from the answer key, I just don't know how to figure it out.An insurance company examines its pool of auto insurance customers and gathers the following information:1) All customers insure at least one car. 2) 70% of the customers insure...
  42. TheSodesa

    Conditional probability for a random vector

    Homework Statement The probability density function for a random vector ##(X,Y)## is ##f(x,y) = 3x##, when ##0 < y< x < 1##. Calculate the conditional probability P(X> \frac{1}{2} | Y > \frac{1}{3}) Homework Equations Conditional probability: \begin{equation} P(A | B) = \frac{P(A \cap...
  43. R

    I Can Conditional Probability Be Solved Generally with PDFs of Variables?

    Is it possible to solve something like this generally or does it depend on the pdf's of the variables? P(x < f(y) | x > -f(y))
  44. Rampart

    Conditional Probability exercise with dice

    Hey there community, I have a question on an exercise. Actually it is a general question based on it. Here is the exercise: We throw 3 dice. If we know that the sum of these 3 is 10, then what is the probability of at least one of them being 3? Well now, this exercise is very simple. I mean I...
  45. SlowThinker

    B Boy/girl riddle (conditional probability)

    I've found this video about conditional probability: All steps look correctly, but the result does not make any sense. I'm ok with the part about frogs, but not so with the boy/girl computation. To sum it up: 1) I have two children and at least one of them is a boy. What is a probability I...
  46. M

    How Do Different Approaches to Conditional Probability Affect Problem Solving?

    Homework Statement suppose we have 9 balls : 2 red, 3 green, 4 yellow. and we draw 2 balls without replacement, the probability that one of them is red and the other is green is : P(R)P(G\R)+P(G)P(R\G) = (2/9)(3/8)+(3/9)(2/8) i faced a problem in the textbook which says: the probability that a...
  47. N

    Is P(A,B|C) = P(A|C) P(B|C), if P(A,B) = P(A)P(B)?

    As stated in my subject line, I know that P(A|B) = P(A) and P(B|A) = P(B), i.e. A and B are separable as P(A,B) = P(A) P(B). I strongly suspect that this holds with a conditional added, but I can't find a way to formally prove it... can anyone prove this in a couple of lines via Bayes' rules...
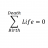
  48. STEMucator

    Calculating the conditional probability of an event

    Hi, I found this screenshot on a website and I thought it was crazy. I want to calculate the conditional probability of this event occurring because it seems so impossible. Assume NLTH is being played. I want to calculate the conditional probability of this hand being dealt. Here is a...
  49. STEMucator

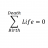
    What is the Conditional Probability for Identifying a Good Item?

    Homework Statement The problem statement is given below: Homework EquationsThe Attempt at a Solution Here is my attempt so far: I'm sure questions 1 - 4 have been answered. Question 5 is what concerns me. I need to find ##P(C' | D')##, which is the probability a good item is...
  50. Linder88

    Conditional probability with marginal and joint density

    Homework Statement Determine ##P(X<Y|x>0)## Homework Equations X and Y are random variables with the joint density function $$ f_{XY}(x,y)= \begin{cases} 4|xy|,-y<x<y,0<y<1\\ 0,elsewhere \end{cases}$$ The marginal densities are given by $$ f_X(x)=2x\\ f_Y(y)=4y^3 $$ The Attempt at a Solution...
Back
Top