Distribution Definition and 1000 Threads

The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution



f
(
x
;

x

0


,
γ
)


{\displaystyle f(x;x_{0},\gamma )}
is the distribution of the x-intercept of a ray issuing from



(

x

0


,
γ
)


{\displaystyle (x_{0},\gamma )}
with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero.
The Cauchy distribution is often used in statistics as the canonical example of a "pathological" distribution since both its expected value and its variance are undefined (but see § Explanation of undefined moments below). The Cauchy distribution does not have finite moments of order greater than or equal to one; only fractional absolute moments exist. The Cauchy distribution has no moment generating function.
In mathematics, it is closely related to the Poisson kernel, which is the fundamental solution for the Laplace equation in the upper half-plane.
It is one of the few distributions that is stable and has a probability density function that can be expressed analytically, the others being the normal distribution and the Lévy distribution.

View More On Wikipedia.org
Recent contents Top users
  1. W

    I Effect of momentum distribution on probability density

    Hi all, I have the following query: I understand that the "make-up" of momentum probability density ##|\tilde{\Psi}|^2## has an effect on the motion of the spatial probability density ##|\Psi|^2##. For example, a Gaussian ##|\tilde{\Psi}|^2## centred far to the right will cause ##|\Psi|^2## to...
  2. J

    DC Distribution System -- Minimum Voltage across the line

    Homework Statement Homework Equations V = IR And R becomes 2(r of one conductor) because of return path. The Attempt at a Solution V minimum is at third junction. At VD Using KVL we get: [/B] Drop at AB = (10 + 20 + 50) * 2 * 0.1 = 16 V Drop at BC = (20 + 50) * 2 * 0.08 = 11.2 Drop at CD =...
  3. M

    MHB Exponential distribution - inequality

    Hey! :o We consider the exponential distribution. I want to show that $$\mathbb{P}\left (\left |X-\frac{1}{\lambda}\right |\leq \lambda \right )\geq \frac{\lambda^4-1}{\lambda^4}$$ I have shown so far that \begin{align*}\mathbb{P}\left (\left |X-\frac{1}{\lambda}\right |\leq \lambda \right...
  4. L

    Calculate a charge distribution given an electric potential.

    Homework Statement Find the distribution of charge giving rise to an electric field whose potential is $$\Phi (x,y) = 2~tan^{-1}(\frac{1+x}{y}) + 2~tan^{-1}(\frac{1-x}{y})$$where x and y are Cartesian coordinates. Such a distribution is called a two-dimensional one since it does not depend on...
  5. Danny Boy

    A Defining Krauss operators with normal distribution

    I am interested in defining Krauss operators which allow you to define quantum measurements peaked at some basis state. To this end I am considering the Normal Distribution. Consider a finite set of basis states ##\{ |x \rangle\}_x## and a set of quantum measurement operators of the form $$A_C =...
  6. G

    I Rewriting of equality in conditional probability distribution

    I don't get $$\frac{P[x<X<x+dx|N=n]}{dx}=f_{X|N}(x|n)$$ Can someone derive why? I would believe that $$f_{X|N}(x|n)=\frac{f(x,N)}{p_n(N)}$$ but I don't get how that would be the same. And I don't get that $$\frac{P[x<X<x+dx|N=n]}{dx}=\frac{P[N=n|x<X<x+dx]}{P[N=n]}\frac{P[x<X<x+dx]}{dx}$$ Can...
  7. S

    Poisson Distribution -- Rental of a number of television sets

    Homework Statement A dealer has a stock of 6 similar television sets which he rents out to customers on a monthly basis. It is known from past experience of the dealer that the monthly demand for the television sets have a Poisson distribution with mean 3.56 (i) Find the probability that in any...
  8. W

    Motion of a particle from its momentum distribution

    Hi all, I recently learned the concept of Maxwell's speed distribution and became interested in how to use similar momentum distributions to study the probabilistic motion of a classical free particle. I have done some of my own reading on probabilities and distributions (no formal lessons yet)...
  9. T

    Poisson distribution ( approximation)

    Homework Statement The number of flaws in a plastic panel used in the interior of cars has a mean of 2.2 flaws per square meter of panel . What's the probability that there are less than 20 surface flaws in 10 square meter of panel ? Homework EquationsThe Attempt at a Solution This is a...
  10. Danny Boy

    A Quantum measurement operators with Poisson distribution

    The following is a somewhat mathematical question, but I am interested in using the idea to define a set of quantum measurement operators defined as described in the answer to this post. Question: The Poisson Distribution ##Pr(M|\lambda)## is given by $$Pr(M|\lambda) =...
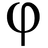
  11. PhiowPhi

    ANSYS - Maxwell, current distribution plot?

    I was modeling current distribution in a component: And I plotted the ##\vec J## to simulate & understand the current distribution throughout the conductor, all the flows make sense, however, at the edge of the conductor like so: Current would distribute all around the area, which is...
  12. T

    Does a Wire in an AC Circuit Have a Surface Charge Distribution?

    I have a simple AC circuit. For example a battery with a capacitor. In the steady-state the capacitor has the same V of the battery. The wire that connect the two components is a very small cylindrical conductor, so it should have a surface charge distribution. It's that correct ? If no, why ?
  13. S

    MHB Understanding Sample Proportions and the Binomial Distribution

    Hi, I am doing a past paper but I am kinda stuck on one of the questions. These are the answers I have: 2a. 225/260 = 0.8654 2b. 32/260 * 4/32 = 0.01407 2c. 32/260 * 28/32 + 228/260 * 221/228 = 0.9577 Then for 2d, I have no idea what to do. Am i suppose to draw one of those probability...
  14. M

    MHB Normal and exponential distribution

    Hey! :o I am looking at the following: 1) A machine produces $100$ gram chocolate. Due to random influences, not all bars are equally heavy. From a long series of observations it is known that the mass X of a chocolate is distributed normally with parameters $\mu = 100$g and $\sigma = 2.0$g...
  15. Pushoam

    Derivation of Bernoulli Binomial distribution

    Homework Statement Derive the bernoulli binomial distribution.Homework EquationsThe Attempt at a Solution Each bernoulii trial could have only two possible outcomes . Let’s name one outcome as success and another outcome as failure. Let’s denote the probability of getting success and failure in...
  16. M

    Automotive How to find the uneven weight distribution on 4 wheels

    Hello, I am working on a project where I am trying to find the weight distribution on a 4 wheeled vehicle that is traveling diagonally up an incline. You can effectively think of the vehicle as having a pitch and a yaw angle in the body frame. Using an arbitrary location of the total center of...
  17. T

    I Laue Diffraction Intensity Distribution

    I am trying to experimentally determine the atomic scattering factors for NaCl using Laue photography. For an NaCl crystal, the intensity of the wave scattered at the unit cell is proportional to (4⋅(fCl+fNa))2 if h,k,l are even and to (4⋅(fCl-fNa))2 if h,k,l are odd. fNa and fCl are the atomic...
  18. T

    Understanding Probability: A Review of Elementary Concepts for Scientists

    Homework Statement I'm asked to find the P (T < ?? ) , v= 26 , α = 0.005 2. Homework Equations The Attempt at a Solution From the table , we could notice that P (T > 2.779) , v= 26 , α = 0.005 , So , i think the ans should be P (T < -2.779 ) , v= 26 , α = 0.005 , But the ans is P (T <...
  19. N

    E(X^r) from Weibull Distribution is equal to Gamma Fn

    Homework Statement I have f(x) = BxB-1e-x^B I need to show that E(Xr) = Ƭ(Gamma)(R/B + 1) Homework Equations I know that E(Xr) = f(x) The Attempt at a Solution Attempt at part of solution I started by saying let u = xB so du = BxB-1dx Can I say then that if u = xB, then Xr = ur/B...
  20. B

    I Center of Image - Brightness Distribution

    Hello, I am reading a review on weak gravitational lensing (https://arxiv.org/pdf/astro-ph/0509252.pdf) and they define the center of an image as follows: $$\vec \theta_c = \frac{\int d^2 \theta I(\vec \theta) q_I [I(\vec \theta)] \vec \theta}{\int d^2 \theta I(\theta) q_I[I(\vec \theta)]}$$...
  21. S

    I Plotting a far-field Intensity distribution

    Hey, I'm attempting to plot a far-field intensity distribution using theoretical values, however I'm having difficulty with calculating the intensity using the following equation: $$I = I_o \frac {sin^{2}{b}}{b^{2}} \frac {sin^{2}{Ny}}{sin^{2}{y}}$$ where: $$y = \frac {kdX}{2f}$$ $$b =...
  22. C

    Determine whether the PDF converges in distribution

    Homework Statement Let $$ \it{f}(x) $$ be a probability density function. Now let Xn have the density: $$ \it{f}_{n}(x) = n\it{f}(nx) $$ Determine whether or not Xn converges in distribution to zero. (this is the verbatim statement, there is no additional information given)Homework...
  23. M

    MHB Defining a Probability Distribution with Measure Spaces and Delta Functions

    Hey! :o Let $M$ be a measure space and $(a_i)_{i\in \mathbb{N}}\subset M$. I want to show that for positive $p_1, \ldots , p_n$ with $\displaystyle{\sum_{i=1}^np_i=1}$ by $\displaystyle{Q=\sum_{i=1}^np_i\delta_{a_i}}$ a probability distribution is defined. Do we have to show that...
  24. binbagsss

    What is the Solution to Part B of the Charge Distribution Integral Homework?

    Homework Statement part b of below [/B] Homework Equations ##(1+x)^{1/2}=1+\frac{1}{2}x-\frac{x^{2}}{8}+...## The Attempt at a Solution [/B] ##\int\limits^{\Lambda}_{-\Lambda} \frac{dy}{\sqrt{r^2+y^2}}=log(\lambda+\sqrt{\lambda^2+r^2}) - log(-\lambda+\sqrt{\lambda^2+r^2}) ## ##=...
  25. M

    Calculating Certain Properties from Distribution Functions

    1. The problem statement, all variables, and given/known data I am given a distribution function f(x) that tells me the number of objects with a certain physical property x (such as having a certain mass or temperature) and I need to calculate the total number of objects, the average value of...
  26. T

    I Proving a multivariate normal distribution by the moment generating function

    I have proved (8.1). However I am trying to prove that ##\bar{X},X_i-\bar{X},i=1,...,n## has a joint distribution that is multivariate normal. I am trying to prove it by looking at the moment generating function: ##E(e^{t(X_i-\bar{X})}=E(e^{tX_i})E(e^{-\frac{t}{n}\sum_{i=1}^n X_i})## I am...
  27. King_Silver

    Mixed random variable distribution question

    Homework Statement See attached image (See below) Homework Equations Differential equations. And a combination of discrete & continuous distributions The Attempt at a Solution The Continous Distribution Function (CDF) is given in the question. So I differentiated it with respect to x...
  28. King_Silver

    How Does the Poisson Distribution Calculate Tornado Probabilities in Georgia?

    Homework Statement The number of tornadoes per year, in Georgia, has a Poisson distribution with a mean of 2.4 tornadoes. Calculate the probability that in any given year, there will be: (i) At most 2 cases. (ii) At least one case. (iii) Calculate the probability that there will be...
  29. M

    How to measure the distribution of weight across a solid object

    Hello, I have a tennis racquet that has a certain weight distribution that makes it play very well. Due to quality control issues from the manufacturer my second racquet of same make and model has a very different weight profile, making matching difficult. I'd like to determine the weight...
  30. R

    Predicted distribution in x generations?

    Homework Statement Consider the stochastic matrix P giving the probabilities of non-college educated households having at least one college educated child. \begin{pmatrix} .9 & .25\\ .1 & .75 \\ \end{pmatrix} If there are currently 300,000 college educated households, and 750000 noncollege...
  31. N

    I Poisson distribution regarding expected distance

    Hi The question is about diseased trees in an area (Poisson process), and states that λ = 15 diseased trees in a km square. I need to calculate expected distance from a point in the square to a diseased tree. Now I thought that this means that P(diseased tree = 0) ~ Po(15) = 3.059 x 10^-7 Or...
  32. L

    I Problems that could occur in estimating n from a Binomial distribution

    Hi, I am doing the following question: https://i.gyazo.com/f2e651334bcbd5f1dcb6d661e4160956.png I have estimated both n and theta. But the part that is throwing me off is what problem could you encounter in estimating n here? My only idea is that it might be something to do with the sample...
  33. D

    I How does the distribution depend on a variable resolution

    Dear all, We were trying to solve the following question but did not quite understand what to do. The question is as follows: The reconstructed invariant mass is usually described by a Gaussian (or Normal) distribution. However, the resolution σ (the width of the distribution) is found to...
  34. G

    I Correlation coeff in conditional distribution

    Can someone derive: ##\frac{Cov(Z+\Theta),\Theta)}{\sqrt{Var(Z+\Theta)Var(\Theta)}}=\frac{\sigma ^2}{\sqrt{1+\sigma ^2}}## My attempt: Numerator: ##Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E[(Z+\Theta-\theta)(\Theta-\mu)]## The denumerator is pretty simple: ##\sqrt{(1+\sigma ^2)\sigma ^2}##
  35. A

    Uneven distribution of charge on a ring problem

    1. 2. I'm totally lost on this problem. Tried guessing in several ways but couldn't come up with the right answer.3. Since I was totally mesmerized by this problem, I need someone to solve it and provide explanation of critical steps of the process. Can someone help me?
  36. A

    I Negative values for Gaussian Distribution

    So in my Physics lab, we divided into groups and our task was to throw darts on a target containing 13 bins. The bins look something like the image below. At the end, our class combined our average, standard deviation, and standard error. I made a Gaussian Distribution and I noticed that the...
  37. T

    Changing distribution when going through a potential

    If we had a a sample of atoms in thermal equilibrium at a temperature, T, it would approximately follow a Maxwell-Boltzmann distribution and be isotropic. But if we now subject these atoms to a force in one direction (e.g. gravity, perhaps near a dense object), it will take the system out of...
  38. U

    Lifting a Beam with a uniform weight distribution

    Homework Statement Hi There, I'm having trouble understanding (what I guess should be) a simple concept and so I can't apply it to a project I'm working on (also kind of rusty on torques and mechanics problems) If I have a hinged beam (of uniform weight) and I lift it from one end and stay...
  39. T

    What Experiment Validated Maxwell's Velocity Distribution?

    Homework Statement What is the name of the experiment that proved Maxwells distribution of velocities? Homework EquationsThe Attempt at a Solution
  40. Pushoam

    Should there be a constant in the RHS of (5.8)?

    Homework Statement Homework EquationsThe Attempt at a Solution I want to ask whether there should be a constant in RHS of (5.8).
  41. R

    Is a symmetric charge distribution the lowest potential

    Is the potential energy of a symmetric planar (x,y) charge distribution lower than any non symmetric distribution ? from the discussion on Gauss's law and symmetric charge distributions I would think so because the electric field could only be normal to the (x,y) plane in the symmetry case but...
  42. Pushoam

    Why Does Calculating Binomial Probabilities Differ from Simple Outcome Ratios?

    Homework Statement I am not getting the above. Let me calculate the probability of getting 2 successes from 5 Bernoulli trials. There are total 10 possible outcomes as each trial has two possible outcomes. The probability of getting one success is P(S1) = No. of successes / no. of total...
  43. M

    A Irradiance distribution of projected beam

    Hey folks, I'm having a little bit of trouble shaking the rust off of my radiometry. I'm projecting a circular beam of some known divergence and power onto a surface angled relative to the center of the beam. Say holding a flashlight, with a cone of half angle θ, at my waist some height h off...
  44. T

    Performing Metropolis-Hastings algorithm for a Poisson Distribution

    Homework Statement The number of busy lines in a trunk group (Erlang system) is given by a truncated Poisson distribution. I am asked to generate values from this distribution by applying the Metropolis-Hastings algorithm. Homework Equations The distribution is given in the attached picture...
  45. P

    MHB James' question about Normal Distribution

    (a) We are told $\displaystyle \begin{align*} \textrm{Pr}\,\left( X < 3 \right) = \textrm{Pr}\,\left( Z < a \right) \end{align*}$, so if $\displaystyle \begin{align*} x = 3 \end{align*}$ and $\displaystyle \begin{align*} z = a \end{align*}$ then we have $\displaystyle \begin{align*} z &=...
  46. P

    MHB James' question about a continuous probability distribution

    Since it's a PDF, that means the entire area under the curve must be 1, so $\displaystyle \begin{align*} \int_0^1{ a \left( x^2 + b \right) \,\mathrm{d}x } &= 1 \\ a \left[ \frac{x^3}{3} + b\,x \right] _0^1 &= 1 \\ a \left[ \left( \frac{1^3}{3} + b\cdot 1 \right) - \left( \frac{0^3}{3} + b...
  47. Z

    Total volumetric charge distribution of the universe

    Greetings! I'm new here and I think about this place as soon as I see what the statement asks. Homework Statement Considering the volumetric density ρv=(e-2r/r2), figure the total charge (ℚ) of the universe. Homework Equations [/B] ρv=ΔQ/ΔV -> (ΔQ ∝ ΔV) ℚ=∫v ρv dxdydz The Attempt at a...
  48. arkaddas

    AC Mains Distribution energized from multiple AC voltage sources

    Even though its possible to keep a bus charged from more than one AC voltage sources, what can be the consequences of doing so? My thoughts: - Assuming thst both the sources have similar (but not equal) phase and magnitude, we can expect small circulating currents. Which brings into question the...
  49. Wrichik Basu

    Neutral wire in electric power distribution between substations

    I had learned from a book in a lower class that electric power distribution from the generating station is done in phases. Like in India, we have three phases of power transmission: the red, green and yellow colours distinguish the three phases. I believe the same is the case in any other...
  50. S

    Charge distribution on spheres

    Homework Statement Two conducting spheres having same charge density and with radius “R” & “2R” are brought in contact and separated by large distance. What are their final surface charge densities ? Homework Equations No equation in question. The Attempt at a Solution Tried using the fact...
Back
Top