Non-linear Definition and 340 Threads

In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one.
In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the unknown variables or functions that appear in them. Systems can be defined as nonlinear, regardless of whether known linear functions appear in the equations. In particular, a differential equation is linear if it is linear in terms of the unknown function and its derivatives, even if nonlinear in terms of the other variables appearing in it.
As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such as solitons, chaos, and singularities are hidden by linearization. It follows that some aspects of the dynamic behavior of a nonlinear system can appear to be counterintuitive, unpredictable or even chaotic. Although such chaotic behavior may resemble random behavior, it is in fact not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout. This nonlinearity is one of the reasons why accurate long-term forecasts are impossible with current technology.
Some authors use the term nonlinear science for the study of nonlinear systems. This term is disputed by others:

Using a term like nonlinear science is like referring to the bulk of zoology as the study of non-elephant animals.

View More On Wikipedia.org
Recent contents Top users
  1. O

    Finding general solution of non-linear, homogeneous ODE

    Homework Statement Find the general solution to x3y'''-9x2y''+76xy'=0 Homework Equations I'm kind of confused on where to start. I'd suppose you'd throw in y=emx but I'm not positive since there are Xs in there. Once I know what to do with the x terms, I can just find all the roots and that'll...
  2. T

    Numerical Simultaneous Solution of Non-Linear Coupled Equations

    For the solution to this problem, I have reduced the number of equations down from 17 to 6. Due to algebra reasons, these equations cannot really be solved symbolically (MAPLE tried, and return four full pages packed with symbols, just for one equation). These three equations need to be solved...
  3. Jonathan Scott

    Why does gravity have to be non-linear?

    I know that Newtonian gravity as a theory is linear and GR is not, but I'm trying to get a feel for why textbooks often insist relativistic gravity must be non-linear, in order to account for the gravitational effect of "gravitational energy" itself (which is however not part of the source term...
  4. B

    Non-Linear Oscillator: Understand & Determine Ring Pendulum

    Can someone please explain to me in layman's terms what a non-linear oscillator is? I need to determine if a ring pendulum is a non-linear oscillator, but I can't really do that without knowing what it is I am describing.
  5. T

    Inhomogenous NON-linear differential equation

    I'm having some trouble solving an equation that is similar to a Bernoulli equation. It is of the form \begin{equation} \ddot{x}+f(x)\dot{x}^2 = g(x) \end{equation} Where x is a function of time, perhaps. I feel moderately certain that there should exist an exact solution, but I've so...
  6. P

    How can I solve this non-linear second order differential equation?

    u''+u'/x+C=0 u-function of x, C - const could someone solve it for me or at least give a hint??
  7. S

    Non-Linear Differential Equation Help

    Consider the system: \frac{dx}{dt} = y and \frac{dy}{dt}= x + 2 x^3 a) Show that the equilibrium solution x=0, y=0 of the linearized system \dot{x} = y, \dot{y}= x is a saddle, and draw the phase portrait of the linearized system. b) Find the orbits of the system and draw its phase...
  8. S

    Non-Linear Differential Equation and Phase Plane Help

    Consider the system: \frac{dx}{dt} = y and \frac{dy}{dt}= x + 2 x^3 a) Show that the equilibrium solution x=0, y=0 of the linearized system \dot{x} = y, \dot{y}= x is a saddle, and draw the phase portrait of the linearized system. b) Find the orbits of the system and draw its...
  9. Q

    Non-linear Operators: Physical Reasons Explained

    Hi, I was wondering: What is the physical reason for only choosing linear operators to represent observables?
  10. H

    Non-linear differential equation

    Hi I'm writing a function (matlab) in my numerical analysis class that descripes in a certain way a non-linear differential equations with Robin BC that I will then feed to a program that uses finite difference method to solve it. It seems to work but I wanted to look for a site or program that...
  11. S

    MATLAB MathCAD/MatLab program for non-linear spring-mass-damper system

    Homework Statement The cutting force developed during a particular machining operation is shown in figure (a). Model the system as a SDF with equivalent mass of the cutting head = 25 kg. The damping is linear viscous (ξ = 0.1), and the equivalent spring is nonlinear “hardening” spring of...
  12. L

    Solving a Non-Linear ODE: What Method Should I Use?

    Homework Statement Solve y'=x^2+y^2 with initial condition y(0)=1. Homework Equations This is a first order ODE. The Attempt at a Solution I have tried separable variable, exact, and homogeneous and non-homogeneous, but none of them work. It's neither linear nor Bernoulli...
  13. P

    Forced undamped non-linear oscillator

    Homework Statement The equation of motion of a forced undamped non-linear oscillator of unit mass is given by a+s(x)=Focoswt. Writing s(x)=s1x + s3x3, where s1 and s3 are constant, choose the variable wt= ϕ, and for s3<<s1 assume a solution x=\sum(n=1 to ∞)(ancos[(n/3)ϕ]+bn sin[(n/3)ϕ]) to...
  14. T

    Invertible Non-Linear Transformation

    Homework Statement Is this invertible? If so, find the inverse. \left( \begin{array}{ccc} y_{1} \\ y_{2} \end{array} \right) = \left( \begin{array}{ccc} x_{1}^{3} \\ x_{2} \end{array} \right)Homework Equations The Attempt at a Solution I know that an invertible LINEAR transformation is a...
  15. mnb96

    How to Compute the Mean of a Non-linear Estimator?

    Hi, let's suppose we are given N statistically independent samples x_1,\ldots,x_n from a certain distribution f_X(x;\theta) depending on a parameter \theta. We are also given an estimator for \theta defined as follows: \hat{\theta}}(N) = \min\{ x_i \\ : \\ i=1..N \} How am I supposed to...
  16. B

    Non-linear LinesHow to Avoid Lying, without Confusing.

    "Non-linear Lines". How to Avoid Lying, without Confusing. Hi, everyone: I will be teaching an intro course in Linear Algebra this Spring. Problem I am having is that the definition of linear does not apply to lines that do not go through the origin: Let...
  17. I

    Solving System of Non-Linear Diff. Equations

    Hi, I'm new to this forum. It looks like an amazing source of information and people here seem to be helpful and knowledgeable. Briefly, I'm an undergrad student currently studying Mechanical Engineering at Concordia University, Montreal, Canada. The first equation seems a bit tricky...
  18. C

    Is there a link between non-locality and non-linearity?

    Is there a strict connection between non-locality and non-linearity? Is it true that non-local systems must have non-linear equations? Are non-linear equations the consequence of non-locality?
  19. O

    Difference between linear and non-linear first order DE

    Some really basic questions about first order DE, which I can't seem to get. What is the difference between a linear and non-linear first order differential equation? For example: dy/dx = cos y dy/dx = cos x And if it's a non-linear first order DE, how do you tell whether it's...
  20. S

    Non-Linear Lever Examples: Get the Answers Here

    Firstly, this is a great forum! Maybe this is more of a mechanical engineering question, but ... Can someone help give me some examples of non-linear levers? I want to be able to stretch a rubber band with factored-increasing force. Like a reversed camber on a compound bow. I hope I...
  21. B

    Bounds for non-linear recursive sequence

    Homework Statement We are given the real sequence x_n+1 = (x_n)^2 - 100 + sin(n), some x_0 Prove that if the sequence is bounded with positive numbers, then necessarily 10 <= x_n <= 11 for all n>=0. Homework Equations The Attempt at a Solution I tried induction and...
  22. A

    Work done by force on a non-linear track.

    We have a force which changes according to what point you're at, e.g: f=(4x²,3z-2y,2z), we need to calculate the work done by this force from point (0,0,0) to (2,1,3) on different curves I don't want an answer I just want an explanation for how this is done, this is what I understand so far...
  23. R

    Extension of Variation of Parameters to First Order Non-Linear ODE?

    The equation of motion of a rocket with mass depletion during ascent and subject to drag forces can be written as M(t) dV/dt = A - M(t)g - BV^2 (Eq. 1) with initial condition V(t=0) = 0 (V is velocity and t is time) Let us assume a linear mass depletion according to...
  24. I

    Non-linear dynamics approach to a manifold of a saddle point using power series

    Homework Statement Im taking a dynamics course and I am using The strogatz book Non-linear Dynamics and Chaos I need to solve a problem that is similar to problem 6.1.14 Basically it consist in the following You have a saddle node at (Ts,Zs) which is (1,1). Consider curves passing through...
  25. M

    Find solutions to non-linear equation

    Question: (t-1)^4+5=3 I know the answer to the question states that there are no solution, but I would like to understand the intuition behind this. If I had this in a test I would waste ages trying to work out why I couldn't solve it. Any advice would be heaps appreciated. Thanks...
  26. A

    Can Non-linear Systems be Solved Analytically?

    Hello, I have numerically solved the system below: dalpha/dx = -beta/(c_1) dbeta/dx = -(c_2)*beta/(c_1)+(c_3)*gamma*dgamma/dx dgamma/dx = (c_4)*[alpha^(c_5)]/c_2 where c_1, c_2, etc. are specified constants. If one plots beta as a function of x, there's a peak. I would like to use...
  27. Rasalhague

    Non-linear forms & tensor densities

    Tensor densities are normally defined in terms of coordinate transformations. Could they also be defined as functions of p tangent vectors and q cotangent vectors, just as tensors are defined, except relaxing the condition of linearity? Can anyone suggest a good, basic introduction to...
  28. Topher925

    Solve third order, non-linear, ODE with indefinite BC's?

    I have a third order, non-linear, homogeneous, constant coefficient ODE that I need to solve but have no idea how to do it. To make matters worse, one of the boundary conditions are indefinite. Here's the equation, y''' + y*y'' - y'^2 + 1 = 0 and the BC's y(0) = 0 y'(0) = 0 y'(\infty) =...
  29. F

    Non-Linear DiffEq: Solve y''+(y')2+1=0

    Homework Statement Solve the given differential equation by using the substitution u=y' y''+(y')2+1=0 The Attempt at a Solution If I got to this last integral correctly, I don't know how to solve it. I'm thinking I didn't get to that step correctly.. But I can't find my mistake..
  30. cepheid

    Coupled 2nd-Order Non-linear ODEs

    Homework Statement I'm trying to solve the equations: \ddot{\phi} + 2\left(\frac{\cos \theta}{\sin \theta}\right) \dot{\theta}\dot{\phi} =0 and \ddot{\theta} - \sin \theta \cos \theta \dot{\phi^2} =0 for \theta(\lambda), \phi(\lambda) where the dots represent differentiation w.r.t...
  31. N

    First Order Non-Linear Differential Equation

    Homework Statement (x+y)dx-(x-y)dy=0 Homework Equations The Attempt at a Solution The solution is c=arctan^-1(y/x)-(1/2)*ln(x^2+y^2) but I don't know how to get the answer. If someone could explain how to solve the above DE, that would be great.
  32. J

    Non-linear Differential Equation - Pulling my Hair

    Non-linear Differential Equation - Pulling my Hair ! Hi, What seems like a simple problem could be going abit better. Any ideas would be sincerely appreciated. (y'')^2 -xy'' + y' = 0 The squared term is causing me grief ! If I set say v = y' , that still leaves me with the squared term...
  33. M

    Non-Linear First Order ODE: Critical Point Linearization

    Homework Statement dx/dt = x - y + (x^2) - xy dy/dt = -y + (x^2) - Determine the critical points for the equation, - Determine the linearized system for each critical point and discuss whether it can be used to approximate the behaviour of the non-linear system. What is the type and...
  34. X

    Help with solving a first order linear and first order non-linear

    Here is an image of the first order linear differential equation and my attempt to solve it. It ends in an integral that can not be solved. http://img831.imageshack.us/img831/9937/math1.gif And here is an image of the first order non-linear differential equation and my attempt to solve...
  35. FeDeX_LaTeX

    Solving Non-Linear Recurrence Relation?

    Hello; I do not have any experience in solving non-linear recurrence relations, so I was just wondering how one solves them. For example, consider the sequence: 1, 2, 6, 15, 31, 56 In general, F_{n+1} = F_{n} + n^{2} Do I still substitute F_{n} = k^{n}? Thanks.
  36. C

    Non-linear ODE: y'=(y-1)^2 + 0.01

    Homework Statement y' = ( y - 1 )^2 +0.01 y(0)=1 (trying out latex) y' = (y-2)^{2} + 0.01; y(0)=1 Homework Equations Separation of variables, Right? The Attempt at a Solution The solution is is y(x)=1+0.1 Tan (0.1x) How did they get this? I did separation of variables...
  37. L

    A non-linear program, truck stops and camps

    I could use some help starting my homework. The problem set up is as follows: #1: Facility Location Suppose we want to locate an airstrip somewhere in the desert where airplanes can land to drop off food aid, which will be trucked to various refugee camps. The camps are located and...
  38. M

    Help toward solving second order non-linear differential equation

    Hi, I have a differential equation of the form d2 x ---------------- = g/z * x(t) dt2 Here g and z are constants. So, this is a 2nd order ODE which has a closed form solution. In fact, i know the solution for x in terms of cosh and sinh functions. In the above differential...
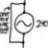
  39. jegues

    Another non-linear device question

    Homework Statement See figure. Homework Equations The Attempt at a Solution I tried KVL (see figure), but still got stuck with only 1 equation and two unknowns. Any ideas/tips on what I should try next?
  40. jegues

    What is the solution to the non-linear device problem?

    Homework Statement See figure Homework Equations The Attempt at a Solution Again, see figure I tried something and it looked promising but the answer doesn't work out. Any ideas?
  41. M

    Question About Non-Linear Second Order Differential Equation

    Hi, I just had my ordinary differential equation final exam today (summer class), the exam was fine. We had a bonus question though, it was a nonlinear second order differential equation, we didn't learn anything about those except for one existence and uniqueness theorem. I am curious if I got...
  42. I

    Non-Linear Water Waves: Exploring Properties & Characteristics

    Cheers I am currently studying non-linearity properties of hydrodynamic waves from a purely mathematical stance. At the moment, I am concerned with radiation, modulational instability described by korteweg-De Vries equation (fifth order) and Spatial Instabilities and chaos in a high order...
  43. B

    Solving non-linear second order ODE

    Homework Statement It will be great if someone could show me some options: I need to prove the following: A particle of mass m is attracted toward a fixed point O (the origin) with a force proportional to its instantaneous distance from O raised to a positive integer power, i.e...
  44. A

    Challenging:How to Solve 2 Non-Linear ODEs?

    How to solve two nonlinear ODEs with boundary conditions? Here is the Q:
  45. J

    Finding the equation to a non-linear set of points

    Homework Statement Determine the equation of the following points: (12. 270) (14, 300) (16, 330) (18. 380) Homework Equations The Attempt at a Solution I realized right away that this is not a linear set of points, so it wouldn't work out to just find the slope between two...
  46. A

    Graphing Surfaces with Non-Linear Equations: What Are My Options?

    Im trying to check my answers to a problem, and in the past I've used a 3d grapher to graph functions like f(x,y) = whatever. but now i need to find a tangent plane to a surface at a point. the surface is: x2y+y2z-z2x=1but i don't know how to go about graphing something expressed that...
  47. V

    Easily measurable non-linear physical relationships.

    I've been trying to think of a really good experiment in which the data gathered would be non-linear. The only ideas I've managed to come up with were either way to simple and boring, or way to hard for me to set up and measure accurately. Some examples of experiments include splash radius of a...
  48. M

    Modelling an Aeroplane - Non-Linear Differential Equation

    Hi everyone, Homework Statement I've been having a bit of trouble with my mathematics coursework. We have to model an aeroplane that has just landed with two equations. One prior to braking, one after. I've used a model with a quadratic drag approximation; and I'm not certain if my result...
  49. L

    Non-linear Differential Equations and Psuedo-randomness

    I was thinking about the non-linear Navier-Stokes equation this morning and was briefly browsing a text on the subject. I'm aware that one popular approach to dealing with turbulence is to take averages and look at correlators (which, in turn, can be related to field theory.) Now, one thing...
  50. E

    Finding the General Solution for a Non-Linear ODE: y' = sqrt(2x-y)

    Homework Statement Find the general solution of y'=\sqrt{2x-y} Homework Equations -- The Attempt at a Solution I've tried approaching this equation through several methods, but I can't separate the variables, I can't make it fit the pattern for linear, I can't make it fit the...
Back
Top