Proper time Definition and 153 Threads

In relativity, proper time (from Latin, meaning own time) along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval between two events on a world line is the change in proper time. This interval is the quantity of interest, since proper time itself is fixed only up to an arbitrary additive constant, namely the setting of the clock at some event along the world line.
The proper time interval between two events depends not only on the events but also the world line connecting them, and hence on the motion of the clock between the events. It is expressed as an integral over the world line (analogous to arc length in Euclidean space). An accelerated clock will measure a smaller elapsed time between two events than that measured by a non-accelerated (inertial) clock between the same two events. The twin paradox is an example of this effect.

By convention, proper time is usually represented by the Greek letter τ (tau) to distinguish it from coordinate time represented by t. Coordinate time is the time between two events as measured by an observer using that observer's own method of assigning a time to an event. In the special case of an inertial observer in special relativity, the time is measured using the observer's clock and the observer's definition of simultaneity.
The concept of proper time was introduced by Hermann Minkowski in 1908, and is an important feature of Minkowski diagrams.

View More On Wikipedia.org
Recent contents Top users
  1. D

    I Analyzing Time Dilation in a Spaceship-Mars Scenario

    Here is the simple problem from the book, but I have a hard time understanding how to solve it, or how to think about it. A spaceship flies past Mars with a speed of relative 0.985 c to the surface of the planet. When the spaceship is directly overhead, a signal light on the Martian surface...
  2. M

    I Minkowski metric and proper time interpretation

    Using an example of 1 space dimension and 1 time dimension, consider the metric ##d\tau^2 = a dt^2 - dx^2## near a heavy mass (##a>1##). From what I've read a clock ticks slower near a heavy mass, as viewed from an observer far away. A clock tick would be representative of ##d\tau## right...
  3. KDP

    I What is the proper time of a vertically moving inertial clock?

    Hi. I am looking for an equation for the round trip elapsed proper time of a clock that is initially moving vertically straight up with a given initial velocity, reaches apogee and then returns to the starting location under gravity. I would like to use the external Schwarzschild geometry of a...
  4. J

    I Physical meaning of null spacetime interval

    Hi all, I've been trying to wrap my mind around the physical meaning of null spacetime intervals. I understand the metric of Minkowski geometry. And I understand that photons have no proper time and no reference frame: the spacetime interval between the emission and absorption of a photon is...
  5. P

    B How to compare the proper times of two spatially distant mass points?

    Do all synchronized clocks in a reference system always show the same time? Is this part of the definition of a frame of reference? Have the clocks always passed the same proper time from zero (see below)? Would the knowledge of the proper time of a clock between two events lead to the...
  6. V

    B Triplets Paradox: Is There a Solution?

    One person (A) stays on Earth, while another (B) goes on a long journey and returns later. We can calculate the time interval for A and the proper time interval for B. Let's say we get Δt=100y and Δτ'=50y. We then consider a second traveler (C) going on a different journey, departing and...
  7. K

    I What Is the Proper Time in Curved Space?

    In special relativity we've the invariant ##\begin{aligned} d s^2=&-d t^2 \\ &+d x^2 \\+d y^2+d z \end{aligned}##. For a clock moving along a worldline the above equation reduces to ##\begin{aligned} d s^2=&-d t^2\end{aligned}## , hence we can say that the time measured by the clock moving...
  8. K

    I Solving for Extrema of Proper Time Integral

    The question is to extremize the proper time : ##\begin{aligned}\int d\tau=\int ( dt^{2}-dx^{2}\\ -dy^{2} \\ -dz^2)^{1/2} \end{aligned}## I've studied calculus of variations somewhat and a can solve a similar problem which I found in the mathematical methods book the author Mary Boas. The way...
  9. K

    I Proper Time Interval: Exploring its Definition on Wikipedia

    Wikipedia article on proper time "Given this differential expression for ##\tau##, the proper time interval is defined as ## \Delta \tau=\int_P d \tau=\int \frac{d s}{c} . ## Here ##P## is the worldline from some initial event to some final event with the ordering of the events fixed by the...
  10. H

    I Def Proper Time GR: Half or Integral Along Path?

    In texts on General Relativity, the proper time ##d\tau^2 = -ds^2## (with an appropriate choice of metric signature) is commonly said that the time measured by a timelike observer traveling along a path is given by the integral of ##d\tau## along this path. Of course it's possible to construct a...
  11. Ennio

    I Exploring Proper Time in FLRW Metric: Meaning and Visualization

    The FLRW metric has been introduced to characterize the homogeneity and isotropy of the Universe and accordingly to obtain "easy" manageable solutions in Friedmann equations. The FLWR metric is where the LHS can be written as where is the proper time (despite we know that time is...
  12. G

    I The Length of World Line: Prerequisite for Proper Time

    What is the prerequisite of "the length of world line equals proper time"?C=i?orC=1?If metric is-+++: ##ds^2=-c^2d\tau^2\Rightarrow whenC=i,s=\tau## If metric is +---: ##ds^2=c^2d\tau^2\Rightarrow whenC=1,s=\tau## So,which one?
  13. e2m2a

    I Understanding Lorentz Factor & Proper Time Invariance

    This is still a confusing concept for me. The Lorentz transformation for proper time is expressed as tau = (1-v sq/c sq)^1/2 x coordinate time. Now we are told that tau is an invariant quantity with respect to all moving reference frames. So how can tau be invariant if its value depends on v...
  14. e2m2a

    I Proper Time & 4-vectors: Clarification Needed

    I am confused. My understanding is that proper time is used in 4 vectors analysis because proper time is frame invariant. Every other inertial frame will agree on the same time increment if they use the proper time of that one reference frame. But when you do the Lorentz transformation, the...
  15. cianfa72

    I Global simultaneity surfaces - how to adjust proper time?

    Hi, searching on PF I found this old post Global simultaneity surfaces. I read the book "General Relativity for Mathematicians"- Sachs and Wu section 2.3 - Reference frames (see the page attached). They define a congruence of worldlines as 'proper time synchronizable' iff there exist a...
  16. Wannabe Physicist

    Is There a Flaw in Understanding Proper Time and Time Dilation?

    Let us denote the events in spacetime before the trip has started by subscript 1 and those after the trip is over by subscript 2. So before the trip has begun, the coordinates in spacetime for A and B are ##A = (t_{A_1},x,y,z)## and ##B = (t_{B_1},x,y,z) = (t_{A_1},x,y,z)##. After the trip is...
  17. D.S.Beyer

    B Exploring Proper Time of CMB: What Does it Mean?

    Did some searches through these forums but didn't find this exact question. I'm sure it's already been asked, but I just missed it, my apologies. Please link. I’ll try and ask this question in 3 different ways, and maybe the idea behind it will become apparent. I know that semantics can really...
  18. U

    A question on proper time in special relativity

    Homework Statement:: This isn't a homework but more of a conceptual question. Relevant Equations:: Proper time, ##\tau## Simply put, the proper time between two events as observed in an unprimed frame is calculated along the timelike worldline between the two events. This implies that the...
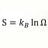
  19. morrobay

    B Time like spacetime interval, proper time, and time dilation

    Since the time like spacetime interval is equal to proper time for stationary or traveling observers, then it seems time dilation (proper time) seen with traveling clock is necessarily frame invariant. Then the so called time between ticks of both identical clocks, with stationary and traveling...
  20. Kairos

    B Is Proper Time Only Perceived by External Observers?

    I am confused about the notion of proper time because it is defined as one's own time measured by one's own clock, but any given person is in all circumstances naturally at rest with respect to himself and therefore his "own proper time" is the coordinate t; am I wrong? So contrary to this...
  21. LCSphysicist

    Proper Time and Time Dilatation

    I am a little confused with the concept of proper time: Using the invariance of the distance square in the Minkowski space, we can get the expression ##d \tau = \frac{d t}{ \gamma}## Now the problem: Aren't the proper time the time measured by a moving clock? That is, if i am moving with speed...
  22. LCSphysicist

    Proper time in an acceleration frame

    $$d\tau = \sqrt{-g_{\mu v}\frac{dx^{\mu}}{d\lambda} \frac{dx^{v}}{d \lambda}} d \lambda $$ Calling ##d \lambda = d t##, t is coordinate time in an inertial frame. $$\Delta \tau = \int \sqrt{-(-1+v^2/c^2)} dt$$ $$\Delta \tau \approx \Delta t - \frac{g^2*\Delta t^2}{6c^2}$$ where $$\Delta t = 2...
  23. F

    Four-momenta trend as a function of proper time

    As a starting point I immediately thought about the equation: ##\frac{dp^\mu}{d\tau}=qF^{\mu\nu}v_\nu## From this I proceed component by component: ##\frac{dp^0}{d\tau}=qF^{0\nu}v_\nu=q\gamma E_yv_y## ##\frac{dp^1}{d\tau}=qF^{1\nu}v_\nu=q\gamma v_yB_z##...
  24. R

    I Proper time to reach the singularity of a Schwarschild black hole

    When calculating the proper time along a timelike radial geodesic, with the initial condition that object the starts at rest at some Schwarzschild coordinate ##r_0>r_S##, i.e. \frac{\mathrm{d}r}{\mathrm{d}\tau}\Bigg|_{r=r_0}=0\;, after using the equations of motion one finds...
  25. J

    Express this trajectory in terms of proper time

    The object moves solely on the $x$-axis, hence I calculated its speed to be $v_x = \frac{dx}{dt} = \frac{c \kappa t}{\sqrt(1+\kappa ^{2} t^2$ Because its speed is not constant, I suppose the Lorentz factor $\gamma = \gamma (t)$, and by plugging in the velocity, I obtain $\gamma = \sqrt(1+ \kappa...
  26. E

    B Rookie question about proper time

    I thought I had a decent basic understanding of this stuff, but it turns out I've got quite a lot of gaps. I drew 3 frames, S, S' and S", where S' and S" move at ##v_1## and ##v_2## w.r.t. S in the ##x## direction, and two different paths to a particular event P: Now the proper time between...
  27. E

    A Time Measurement in Friedman Metric: Physically Possible?

    If a proper time measuring clock goes along for the ride between events, then is such a clock physically possible as the scale factor changes / increases in the Friedman metric? How could any clock have zero spatial changes for that situation?
  28. Physicsphysics

    Finding t and x in terms of proper time?

    I tried finding a.a (four vector inner product) and I got to γ4{(v.a)2(1-γ4v.v - 2γ2) - a.a}, where again a and v are three vectors on the rhs (sorry to be confusing). a.a = g2 since it's a constant. I have no idea where to go from here to find the time and position. Please help!
  29. S

    The definition of the proper time

    I wonder what is the proper time, the time passed on the train or the time of the observer? If there is another people on the train, we see the train as a frame, so is the time on the train the proper time or the time of rest frame?
  30. George Keeling

    I Why do clocks show proper time?

    I often see the assertion that clocks show proper time. (E.g. this thread). But I don't think that I have seen a good reason for the assertion in GR. It's not a problem in SR because one can always find a coordinate system that is stationary relative to a clock so, from the metric, ##...
  31. M

    How Does Acceleration Transform in Special Relativity?

    I'm struggling in the details of this exercise. Let ##S'## be the reference frame where the acceleration of the spaceship is constant, in which case we have ##u'(t')= a' t'## (since we assume no acceleration at the beginning). The rest frame of the rocket ##S## is connected to ##S'## via a...
  32. Pericles98

    I Exploring Proper Time: How David and John Measure Time Differently

    Hello everybody, I've just started studying special relativity and seem to be having a bit of a problem with understanding the concept of proper time. In Modern Physics, by Serway, proper time is defined as the time interval between two events as measured by an observer that sees both events...
  33. T

    How do proper time and time dilation differ?

    Homework Statement I am currently stuck on a problem as shown below. My confusion really come from the fact that I can never seem to understand the difference between proper time and time dilation. As in some books they seem to mean the same thing and never give a clear indication Homework...
  34. I

    I Does the Invariance of Proper Time Lead to the Lorentz Transformation?

    Hi, I've seen several explanations for sr on youtube. But they all start off explaining from a different perspective. I was wondering how the fundamental postulates of sr lead to the invariance of proper time between frames, and also what "order" everything is derived in. For example, does the...
  35. E

    B Calculate Proper Time for Two Events in Special Relativity

    I am refreshing myself on a bit of special relativity and I remember kind of taking the invariance of the spacetime interval for granted the first time. When thinking about it and running some examples I started to get confused so I decided to come here. All of the books I've read always have...
  36. TheQuestionGuy14

    B Difference Between Proper Time and Coordinate Time Explained

    I was reading up on the nature of time and found this: " In one sense, "time" is the time that is in the equations of physics. That's the t in the equations of the paper, it's the parameter that describes how the states of all systems in the universe change." Does this explain coordinate time...
  37. R

    B Proper Time Change: Helium 4 Superfluid Effects

    When helium 4 becomes a super fluid does the proper time change, can this be detected?
  38. Zephaniah

    B Understanding the Meaning of "Proper Time"

    What is proper time? How can I solve proper time? "There is only one frame of reference in which clock is at rest, and there are infinitely many in which it is moving." What does it mean?
  39. F

    B What is the Definition of Improper Time in Special Relativity?

    Hi all, this is just a terminology question. I am aware of the definition of "proper time" (and "proper length") in the context of special relativity. I recently heard the term "improper time", as opposed to proper time, of course. Is that accepted terminology? Sounds weird to me.
  40. binbagsss

    I Coordinate and proper time, null geodesic

    I have a question which asks show that a null geodesic to get to r> R , r some constant, given the space time metric etc, takes infinite coordinate time but finite proper time. ( It may be vice versa ). I just want to confirm that, ofc there is no affine parameter for a null geodesic and so you...
  41. C

    I Nonlinear relation between coordinate time and proper time

    For Schwarzschild geomery $$ds^2=-(1-\frac{2GM}{r})dt^2+(1-\frac{2GM}{r})^{-1}dr^2+r^2d\Omega^2$$ For a Schwarzschild observer , the proper time and coordinate time are related by $$d\tau=(1-\frac{2GM}{r})^{1/2}dt$$ There is a often used relation between proper time and coordinate time $$d\tau...
  42. J

    B Relative motion and proper time

    Hi everyone! Sorry for the bad english! Quick question Just to see if I understood: If a person on a spaceship moving at 0.7c in relation to a person in the earth, and both of then agreed they started making microwave popcorn at the same time (like when the spaceship is just above the head of...
  43. P

    B Understanding Proper Time vs. Layman's Time

    What is proper time? As opposed to time in the layman's term? [Mentors' note: This thread was split from another thread, and when it was a stray irrelevant quote was accidentally included. It has been removed, along with two later posts trying to clear up the confusion introduced by the stray...
  44. B

    Proper time elapsed between a photon being sent and received

    Homework Statement The problem I am trying to solve is the proper time elapsed along A's worldline between a photon being emitted and sent to B (which is a distance L away from it along the x axis) and being reflected and detected by A again. The question is the second part of the question...
  45. S

    I Difference between proper time and coordinate time

    Hello! I found this questions in several places, but no answer made me fully understand it, so I decided to give it one more try here. I am not sure I understand the difference between them in GR. I have a feeling of the proper time as the time measured by the clock of someone moving with a...
  46. E

    B Proving Proper Time of Photon in Friedman Metric

    If I understand it correctly, the proper time differential for a photon in flat space is zero. That is evident if the velocity of light is equal to c, so the right hand side of the Minkowski metric is equal to zero. Therefore the left side must also be zero. My question: Is the same true for...
  47. T

    I Proper time to reach the singularity - rocket acceleration

    I was assuming that the proper time lapse between ##r=2M## and ##r=0## increases with increasing acceleration outwards. According to this paper https://arxiv.org/pdf/0705.1029v1.pdf Fig.2. it turns out however that the proper time to reach the singularity is longer with low acceleration but...
  48. tom.stoer

    A Maximizing survival time when falling into a black hole

    Unfortunately I didn't find a thread discussing this issue. First I will sketch the standard argument that one should not use the rocket engine and try to accelerate away from the singularity. Then I will try to identify the problematic part of this argument and ask for your comments. 1) For...
  49. C

    I Particle at event horizon as black hole evaporates

    If you are observing a particle enter a black hole, you watch its proper time go to zero at the event horizon as it is 'frozen' there from your frame of reference. What happens in your reference frame as the black hole evaporates? While you can't illuminate where the particle is from your frame...
  50. haushofer

    I Gravitational time dilation, proper time and spacetime interval

    Dear all, I'm having confusion about the standard derivation of Schwarzschild's gravitational time dilation. For concreteness I'll follow the explanation of Schutz' "gravity from the ground up", but other texts argue the same. So let me rephrase Schutz's explanation (I surpress factors of c in...
Back
Top