Proper time Definition and 155 Threads
-
S
Proper Time in Special vs. General Relativity
We know that the proper time between two events is the shortest possible time between those two events that can be measured in any frame. This follows from the idea that moving clocks run slow-- a stationary clock at rest in S' which moves relative to S at a constant speed v will be time dilated...- schaefera
- Thread
- General General relativity Proper time Relativity Time
- Replies: 12
- Forum: Special and General Relativity
-
K
Can the proper time interval be < the coordinate time interval?
In general relativity, we have a gravitational time dilation of: \frac{d\tau}{dt} = \frac{1}{\sqrt{1 - \frac{2GM}{rc^2}}} The term - \frac{2GM}{rc^2} appears to be based on the fact that gravity is attractive. If I understand correctly, if the curvature of space-time leads to attraction, then...- kmarinas86
- Thread
- Coordinate Interval Proper time Time Time interval
- Replies: 6
- Forum: Special and General Relativity
-
J
Why particles follow path of extremal proper time?
Hello everyone. I understand how to figure out the paths of the free particles following the principle of extremal proper time, but... where does it come from? I mean, how it's derived that particles follow a path of extremal proper time in space-time? I know that for example in flat space-time...- jorgdv
- Thread
- Particles Path Proper time Time
- Replies: 12
- Forum: Special and General Relativity
-
Y
Reversal of proper time for a falling object
Consider the Schwarzschild line element for radial motion only: c^2 d\tau^2 = \left(1-\frac{2GM}{rc^2}\right) c^2 dt^2 - \frac{dr^2}{ \left(1-\frac{2GM}{rc^2}\right)} Solve for d\tau^2/dt^2: \frac{d\tau^2}{dt^2} = \left(1-\frac{2GM}{rc^2}\right) - \frac{dr^2/dt^2}{...- yuiop
- Thread
- Falling Falling object Proper time Time
- Replies: 49
- Forum: Special and General Relativity
-
N
Proper time in Schwarzschild Space
Please explain me how to find the proper time taken by one twin to travel around a massive body while his other twin stays on the Earth in Schwarzschild space?- Nilupa
- Thread
- Proper time Schwarzschild Space Time
- Replies: 10
- Forum: Special and General Relativity
-
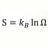
Distance/rate = t = sqrt[2d/a] = Same Proper Time ?
If one clock is moving with constant velocity. The other clock moving with constant acceleration , both with respect to Earth . And both clocks travel the same distance in the same time with respect to earth. distance/rate = [2d/a]1/2 Gamma is given for velocity clock. Would you expect the...- morrobay
- Thread
- Proper time Time
- Replies: 10
- Forum: Special and General Relativity
-
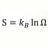
Proper Time : Constant Velocity Clock vs Constant Acceleration Clock
Homework Statement 3 clocks at to A clock on Earth B clock above Earth 4.66 * 1014 meters C clock above Earth 3.30 * 1013 meters B accelerates to .6 c and arrives at Earth when Earth clock reads 2.6 *106 sec = 30 days With velocity 1.8 *10^8 m/sec with gamma = .8 B clock reads 2.07 *...- morrobay
- Thread
- Acceleration Clock Constant Constant acceleration Constant velocity Proper time Time Velocity
- Replies: 5
- Forum: Introductory Physics Homework Help
-
U
Why Does the Spaceship Record the Proper Time in Relativity?
On several homework questions I have encountered the following type of scenario: Two clocks are perfectly synchronized. One is placed in a spaceship, and the other is left on the ground. The spaceship flies to some distant location at some high speed, and then returns to earth. When the...- Undoubtedly0
- Thread
- Proper time Spaceship Time
- Replies: 13
- Forum: Special and General Relativity
-
P
Derivation of Proper Time in General Relativity
In relativity, proper time along a world-line is be defined by d\tau^{2} = ds^{2} / c^{2} However, proper time can also be understood as the time lapsed by an observer who carries a clock along the world-line. In special relativity, this can easily be proven: The line element in special...- paultsui
- Thread
- Derivation General General relativity Proper time Relativity Time
- Replies: 5
- Forum: Special and General Relativity
-
D
Calculating proper time using schwartzchild metric
I am using the schwartzchild metric given as ds^2 = (1 - \frac{2M}{r})dt^2 - (1 - \frac{2M}{r})^{-1} dr^2 , where I assume the angular coordinates are constant for simplicity. So if a beam of light travels from radius r0 to smaller radius r1, hits a mirror, and travels back to r0, I am...- demonelite123
- Thread
- Metric Proper time Time
- Replies: 5
- Forum: Special and General Relativity
-
N
Coordinate and proper time animation
Someone posted this animation in a previous discussion and I just 'rediscovered' it in my notes: http://www.adamtoons.de/physics/gravitation.swf Do you experts think it accurate, and if so, wouldn't this be a nice tool to display coordinate time versus proper time?? [Is it worth...- Naty1
- Thread
- Animation Coordinate Proper time Time
- Replies: 1
- Forum: Special and General Relativity
-
M
Coordinate time and proper time.
Hello, So, I have just started studying relativity, and I am confused about some basic concepts in relativity. So, the book we use says that that time has three different kinds, proper or path time, coordinate time and spacetime intervals. I understand that coordinate time is the same as...- Moataz
- Thread
- Coordinate Proper time Time
- Replies: 26
- Forum: Special and General Relativity
-
H
General relativity- weak field limit and proper time
Homework Statement A satellite is in circular polar orbit radius r around Earth (radius R, mass M). Clocks C on satellite and C0 on south pole of earth. Show the ratio of the rate of C to C0 is approximately 1 +\dfrac{GM}{Rc^2} - \dfrac{3GM}{2rc^2} Homework Equations d\tau =...- hai2410
- Thread
- Field General General relativity Limit Proper time Relativity Time Weak
- Replies: 2
- Forum: Advanced Physics Homework Help
-
T
Reaching the Rindler horizon in a finite proper time
Hi, I am trying to show that timelike geodesics reach the Rindler horizon (X=0) in a finite proper time. The spacetime line element is ds^{2} = -\frac{g^{2}}{c^{2}}X^{2}dT^{2}+dX^{2}+dY^{2}+dZ^{2} Ive found something helpful here...- teeeeee
- Thread
- Finite Horizon Proper time Rindler horizon Time
- Replies: 3
- Forum: Special and General Relativity
-
A
How Fast Must a Meter Stick Move to Appear Half Its Length?
Homework Statement How fast must a meter stick be moving if its length is observed to shrink to 0.5 m? The Attempt at a Solution A meter stick moving at speed V to a stationary observer is the same thing as a stationary meter stick and an observer moving at speed V. Lproper = Lp = 1 meter...- alksjadf
- Thread
- Proper time Time
- Replies: 6
- Forum: Introductory Physics Homework Help
-
A
Time Dilation Problem; Find the proper time, ts.
Homework Statement Alpha Centauri, the closest star to Earth, is 4.3x10^6 m away. How long would it take a spaceship to reach the star if it were traveling at 0.999c? Homework Equations I did get the answer as 0.2a...and the textbook also said it would take about 2 months, I do not...- Ammar SH
- Thread
- Dilation Proper time Time Time dilation
- Replies: 4
- Forum: Introductory Physics Homework Help
-
T
Calculating World Line for Least Proper Time: An Easy Question on Relativity
Hi everyone! Let's take two events P_1,P_2 in a Minkowsky spacetime, and let's choose them both lying on the \omega axis, separated by a certain distance. Now, I want to calculate the world line of the particle which experiences the least proper time during its trip between the two points...- teddd
- Thread
- Proper time Time
- Replies: 3
- Forum: Special and General Relativity
-
J
Determining who measures Proper Time and Length
It has REALLY been bugging me lately. I'm studying Einstein's Special Rel and am finding it annoying to determine who observes the proper length and time in the following conditions: An electron accelerator is 4km long and can accelerate electrons up to speeds of .9999995c. So when asked...- ja_tech
- Thread
- Length Proper time Time
- Replies: 5
- Forum: Special and General Relativity
-
S
Confusion with proper time from different frame of references
I'm having trouble getting my head around the idea of 'proper time'. I've been thinking of this situation and I can't seem to understand what exactly the proper time is. Say we have a planet 'A' and a rocket B moving towards this planet. From the perspective of A, B is moving towards A. If an...- Stevey_R
- Thread
- Confusion Frame Proper time References Time
- Replies: 2
- Forum: Special and General Relativity
-
S
Is Proper Time Relative in Special Relativity?
The idea of proper time has been confusing me. Say for example we have a spaceship with John in it traveling past the Earth, towards a planet called NEC. Ann is on Earth and starts her timer as John travels past the Earth, towards NEC. Ann notes that it takes 2 years for John to arrive at NEC...- Shark 774
- Thread
- Proper time Time
- Replies: 31
- Forum: Special and General Relativity
-

Particle falling into a black hole singularity within a finite proper time
Hello, Can anyone help me with that? It's a problem taken from Wald book on General Relativity,in the section of Schwarzschild solution Thanks Show that any particle (not necessarily in geodesic motion) in region II (r < 2M ) of the extended Schwarzschild spacetime, Figure 6.9, must...- camipol89
- Thread
- Black hole Falling Finite Hole Particle Proper time Singularity Time
- Replies: 2
- Forum: Advanced Physics Homework Help
-
Z
Trying to understand what extremal proper time means.
General relativity states that all free falling bodies follow spacetime geodesics. A geodesic is a path of extremal proper time. My intuition tells me that extremal proper time is the maximum amount of real time. So does this mean that all objects will take the path of most time to get from...- zeromodz
- Thread
- Means Proper time Time
- Replies: 12
- Forum: Special and General Relativity
-
H
Understanding Proper Time in Einstein's Special Theory of Relativity
Howdy! I'm new to Physics Forum and glad to be part of the community. I just finished reading Einstein's Special Theory of Relativity and cannot understand the term 'proper time'. What does it specifically mean? When deriving the equation for length contraction, the author of Giancoli Sixth...- hschia
- Thread
- Proper time Time
- Replies: 14
- Forum: Special and General Relativity
-

Derivation of Proper Time, Speed, and Acceleration in SR
This is a continuation of the thread Derivation of proper time of acceleration in SR We have definitions for proper time, proper speed, proper acceleration, coordinate speed, coordinate time, and coordinate acceleration. 1) What is the definition ofproper distance? 2) If proper...- stevmg
- Thread
- Acceleration Derivation Proper time Speed Sr Time
- Replies: 14
- Forum: Special and General Relativity
-

Derivation of proper time in acceleration in SR
To yuiop: Consider an object of mass m0 which, subjected to a constant force, accelerates at a0 initially. Initially, the velocity of this mass is zero but then picks up as this force is applied. By the relativistic momentum equation, a = dv/dt = a0\sqrt{(1 - v^2/c^2)}...- stevmg
- Thread
- Acceleration Derivation Proper time Sr Time
- Replies: 100
- Forum: Special and General Relativity
-
A
Derivation of Proper Time and Proper Space
I have tried to derive the formula for the proper time from the two equations of the Lorentz Transformation. The formula is as follows (see Wikipedia: http://nl.wikipedia.org/wiki/Eigentijd): tau = t*sqrt (1 - v**2/c**2) The two equations of the Lorentz Transformation are as follows...- AdVen
- Thread
- Derivation Proper time Space Time
- Replies: 17
- Forum: Special and General Relativity
-

Is Proper Time Contraction Valid for Accelerated Watches?
Le K_0 and K_1 be two inertial frames moving relative to each other with velocity v, from Lorentz transfromation we have that a watch(t') at the origin of K_1 is slow(proper time contraction) acording to dt'=dt/gamma=(1-(v/c)^2)^{1/2}dt where v is the velocity of the watch. My question...- facenian
- Thread
- Proper time Time
- Replies: 47
- Forum: Special and General Relativity
-
N
Time Dilation and Proper Time: Calculating the Effects of Relativistic Travel
1. Homework Statement [/b] Just need some help getting started on what looks like a rather simple problem! A rocket travels to a star 5 light years distant, observers on the star time the journey at 6years. I need to find the time recorded on a clock aboard the rocket and the distance to the...- NUFC
- Thread
- Dilation Proper time Time Time dilation
- Replies: 9
- Forum: Introductory Physics Homework Help
-

Is Proper Time in Relativity an Invariant Quantity?
A very basic question, perhaps, but I am starting from basics and checking all my understanding. In Relativity is τ (tau), the proper time experienced by an observer adjacent to a clock in an inertial frame of reference, an invariant quantity? And if not, in what way can it vary?- Grimble
- Thread
- Invariant Proper time Relativity Time
- Replies: 12
- Forum: Special and General Relativity
-
J
Calculating Proper Time for an Object Under Constant Acceleration
Is this the correct way to calculate the proper time that has passed for an object under constant acceleration over the time interval [0,t1]? I just downloaded and started teaching myself how to use LaTex today so bear with me here. I can get the output PDF file but I don't know how to insert...- jacksonwalter
- Thread
- Proper time Time
- Replies: 18
- Forum: Special and General Relativity
-
J
Find the Proper Time Extrema: Twin Paradox Explained
Quick question: Suppose I hold two initially synchronized clocks on Earth and throw one up and catch it when it comes back down. Now my (small amount of) knowledge of GR tells me that the proper time on the thrown clock should be maximized since it was on a geodesic. However, this seems like...- Ja4Coltrane
- Thread
- Extrema Proper time Time
- Replies: 5
- Forum: Special and General Relativity
-
S
How Fast Does a Spaceship Travel from Earth to Pluto and Back in 11 Hours?
Homework Statement A spaceship leaves earth, travels to Pluto (which os 5 hours of distance away at the time), and then returns to Earth in exactyly 11 hours later. assume the spaceships acceleration time is very short so it is always traveling at a constant speed. also assume that Earth and...- sarahaha288
- Thread
- Earth Pluto Proper time Time
- Replies: 1
- Forum: Introductory Physics Homework Help
-
W
Gravitational vs geodesic proper time
I've been trying to learn GR and I've been back and forth through Schutz's first course book. I think I understand the basic principals, but one thing still eludes me: a traveler in free fall travels along the geodesic, the path of longest proper time. If the path between two points passes...- westwood
- Thread
- Geodesic Gravitational Proper time Time
- Replies: 3
- Forum: Special and General Relativity
-
T
Is Proper Time Invariance Proven?
is proper time invariant? proof? thanks...- thoughtgaze
- Thread
- Invariance Proper time Time Time invariance
- Replies: 3
- Forum: Special and General Relativity
-
M
Writing Equations of Particle Trajectories in Proper Time
Homework Statement I have the trajectories of a particle in the space-time: \tau(\sigma) = \frac{1}{a}senh(\sigma) x(\sigma) = \frac{1}{a}cosh(\sigma) How can I write this equations depending on proper time t of the particle? Homework Equations The Attempt at a...- martyf
- Thread
- Particle Proper time Time Trajectories Writing
- Replies: 13
- Forum: Advanced Physics Homework Help
-
A
Proper time of an accelerating particle
A particle has a constant acceleration in a laboratory from 0 to 0.5c in 3 seconds. What time elapses for the particle (i.e. what is the proper time for the particle)? Hint: (you will have to integrate the proper time of the particle over the 3 seconds as measured in the laboratory frame)...- alienslag
- Thread
- Particle Proper time Time
- Replies: 3
- Forum: Special and General Relativity
-
L
Constantly accelerating object and its proper time
The question is: A rocket has a constant acceleration in a rest frame that is 0 to 0.8c in 4s. What is its proper time? This question I found, I guess I'll have to use integration but don't have a clue where to start off. Could you give me some ideas please?- lhy56839
- Thread
- Proper time Time
- Replies: 9
- Forum: Special and General Relativity
-

What is the proper time interval in special relativity?
In Tipler & Mosca: Physics for Scientists and Engineers, e5, extended edition (page R-14 of the supplementary section on special relativity), there is a question: “You are standing on a corner and a friend is driving past in an automobile. Each of you is wearing a wrist watch. Both of you...- Rasalhague
- Thread
- Physics Proper time Time
- Replies: 5
- Forum: Special and General Relativity
-

What is the role of proper time in quantum theory
What role does proper time play in quantum theory? Does proper time have any meaning in QM? By quantum theory I should perhaps say "relativistic quantum mechanics" since I don't know enought QFT to ask a proper question. If there were a proper time \tau parameter or dynamical variable...- pellman
- Thread
- Proper time Quantum Quantum theory Theory Time
- Replies: 14
- Forum: Quantum Physics
-
H
Proper Time For Photon on Null Geodesic
I can understand the logic from some arguments as to why proper time in a photon's "frame of reference" is zero. I cannot understand how this follows from the argument that (SPACE)2 - (TIME) 2 = 0. This to me says that the SPACE-TIME interval for the photon is zero (null interval) and SPACE =...- Hacky
- Thread
- Geodesic Photon Proper time Time
- Replies: 3
- Forum: Special and General Relativity
-
F
Spacetime diagrams and proper time
Hey guys, Can someone please explain to me this image: http://www.astro.ucla.edu/~wright/omega0.gif from the page http://www.astro.ucla.edu/~wright/cosmo_02.htm What i do understand: I understand the concept of light cones I understand that the units used for the axes means the lines...- FunkyDwarf
- Thread
- Diagrams Proper time Spacetime Time
- Replies: 3
- Forum: Cosmology
-
Newie relativity question: proper time vs. arc length?
Doran/Lasenby define a proper interval as: \delta \tau = \int \sqrt{\frac{dx}{d\lambda} \cdot \frac{dx}{d\lambda}} d\lambda (c=1, x= (t,x1,x2,x3) is a spacetime event, and the dot product has a +,-,-,- signature) and say that this is called the proper time. I can see that this...- Peeter
- Thread
- Arc Arc length Length Proper time Relativity Time
- Replies: 8
- Forum: Special and General Relativity
-
S
How Does Proper Time in Radial Free Fall Differ from Newtonian Predictions?
Foster and Nightingale give an equation for the proper time of a radially falling clock between any two distances. (Short Course in General Relativity, 1979, p. 128.) As they state, the equation is the "same as its Newtonian counterpart." So there are no factors representing any slowing of the...- Stoonroon
- Thread
- Fall Free fall Proper time Radial Time
- Replies: 2
- Forum: Special and General Relativity
-
I
Special Relativity, accelerating frames, proper time
Homework Statement A particle has a constant acceleration in a laboratory from 0 to 0.5c in 2 seconds. What time elapses for the particle (i.e. what is the proper time for the particle)? Hint You will have to integrate the proper time of the particle over the two seconds as measured in the...- iamaelephant
- Thread
- Frames Proper time Relativity Special relativity Time
- Replies: 3
- Forum: Introductory Physics Homework Help
-
Y
Proper time of accelerated clocks
In other threads the topic of how the proper time of a clock under acceleration has come up a number of times so I have decided to analyse this subject in a little more detail. For this analysis we have these conditions: a)Two clocks are initially at rest separated by a distance L_o along...- yuiop
- Thread
- Clocks Proper time Time
- Replies: 18
- Forum: Special and General Relativity
-
N
How Does Delta S Relate to Proper Time in Special Relativity?
Homework Statement If the spacetime interval (delta S)^2 > 0, show that delta t=deltaS/c is the proper time between the two events. Homework Equations Can anyone please explain to me how I should be approaching this problem. I have been working on it for a while with no success. I was...- nwdavis1
- Thread
- Proper time Time
- Replies: 2
- Forum: Advanced Physics Homework Help
-
D
How Does Time Dilation Affect Flight Duration in Special Relativity?
Homework Statement A plane flies with a constant velocity of 208 m/s. The clocks on the plane show that it takes exactly 2.00 hours to travel a certain distance. Calculate how much longer or shorter than 2.00 h this flight will last, according to clocks on the ground. ________s Homework...- deenuh20
- Thread
- Proper time Relativity Time
- Replies: 1
- Forum: Introductory Physics Homework Help
-
B
Is Proper Time a Relativistic Invariant?
do you kinow a simple and convincing argument for the fact that proper time is a relativistic invariant?- bernhard.rothenstein
- Thread
- Invariance Proper time Relativistic Time
- Replies: 4
- Forum: Special and General Relativity
-
B
Proper time or proper time interval
i find in the literature in different textbooks the term proper time Thomas A. Moore, Six Ideas that Shaped Physics (McGraw-Hill) 1998 and the term proper time interval Yuan Zhong Zhang, Special Rekativity and its Fundamental Foundations, (World scientific ) I consider that the first is...- bernhard.rothenstein
- Thread
- Interval Proper time Time Time interval
- Replies: 3
- Forum: Special and General Relativity
-
M
Proper time for an object falling into a black hole
How do you calculate the proper time and the proper distance for an object free falling into a black hole from the event horizon to the singularity?- MeJennifer
- Thread
- Black hole Falling Hole Proper time Time
- Replies: 5
- Forum: Special and General Relativity