Rolling Definition and 1000 Threads

Rolling is a type of motion that combines rotation (commonly, of an axially symmetric object) and translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding.
Rolling where there is no sliding is referred to as pure rolling. By definition, there is no sliding when there is a frame of reference in which all points of contact on the rolling object have the same velocity as their counterparts on the surface on which the object rolls; in particular, for a frame of reference in which the rolling plane is at rest (see animation), the instantaneous velocity of all the points of contact (e.g., a generating line segment of a cylinder) of the rolling object is zero.
In practice, due to small deformations near the contact area, some sliding and energy dissipation occurs. Nevertheless, the resulting rolling resistance is much lower than sliding friction, and thus, rolling objects, typically require much less energy to be moved than sliding ones. As a result, such objects will more easily move, if they experience a force with a component along the surface, for instance gravity on a tilted surface, wind, pushing, pulling, or torque from an engine. Unlike cylindrical axially symmetric objects, the rolling motion of a cone is such that while rolling on a flat surface, its center of gravity performs a circular motion, rather than a linear motion. Rolling objects are not necessarily axially-symmetrical. Two well known non-axially-symmetrical rollers are the Reuleaux triangle and the Meissner bodies. The oloid and the sphericon are members of a special family of developable rollers that develop their entire surface when rolling down a flat plane. Objects with corners, such as dice, roll by successive rotations about the edge or corner which is in contact with the surface. The construction of a specific surface allows even a perfect square wheel to roll with its centroid at constant height above a reference plane.

View More On Wikipedia.org
Recent contents Top users
  1. A

    MHB Probability of Rolling Sum > 3 with Two Dice

    Two fair dice are rolled. What is the probability of rolling a sum that exceeds 3?
  2. Y

    Rolling pendulum angular acceleration

    -
  3. Pipsqueakalchemist

    Engineering Rigid wheel rolling without slipping -- Trying to find angular acceleration

    So I tried the problem and it’s different from the solution. I’m confused on why my attempt didn’t work, is it because the wheel is undergoing general planar motion? I tried to just apply Newton’s 2nd law to find the acceleration of the centre and then use that to find angular acceleration. The...
  4. J

    Automotive Rolling resistance coefficient on sand

    Hello I,d like to find or to calculate Rolling resistance coefficient on sand tyre 37/12.5 R37. Thanks for your help
  5. dahoom102

    Direction of friction in a yoyo rolling on an inclined plane

  6. P

    Why is static friction not considered in the work-energy theorem?

    My question is this: - Friction exists (for no slipping/pure rolling to occur) - Why is the work done against friction not accounted for in the conservation of energy equation? Thank you!
  7. Hamiltonian

    Rolling ball inside a shell problem

    I was able to solve this problem easily by using the fact that the center of mass of the system is stationary as ##\sum F_{ext} = 0## for the ball and shell system. since COM's of both objects can be replaced with point masses at there center, the shell will have maximum displacement when its...
  8. chucho11028

    Motion in one dimension -- Experiments with a Hot Wheels car rolling down a ramp

    Hello This is not a homework, this is my own experiment to understand how the motion works. Please, follow my question here below: I have a hot wheels race with a slope with 10 degrees where I use a small car which departs from the top to the bottom. I have taken 5 times the time to get an...
  9. R

    Rolling and Sliding: Solving Angular Momentum Theorem

    Hi, I solved this prolem in the following way. I have started with the angular momentum theorem: Iα=fR As the force of friction vector is attached on point of contact of the ball and the supporting surface, the moment of inetria is: Ic= MR^2 + Icm = MR^2 + (2/5)MR^2 Ic*a/R=μMgR tr=7/5(v0/μg)...
  10. ezfzx

    Ball rolling within a rolling cylinder

    Cylinders rolling down inclines are a common demo. But how do you model the movement of a sphere rolling within a rolling cylinder? I teaching a physics class and this question came up and my dynamics math is a little rusty. But I haven't found anything like this in any book or online. There's...
  11. E

    Rolling 3 objects on an inclined plane

    Hello there, I have a question regarding this problem. I have no problem with part A. However, in part B, my solution manual states that the hollow cylinder will reach the bottom last. Why is it? I mean shouldn't the solid cylinder and the hollow one reach the bottom at the same time? you know...
  12. T

    Calculating air resistance for a cart rolling down a ramp

    I am doing a physics lab where we are supposed to calculate air resistance and find the impacts of velocity and cross sectional area on air resistance. For the experiment, we rolled a cart down a ramp and measured data using Pasco Capstone software. When rolling the cart down the ramp, we...
  13. archaic

    Cylinder rolling due to magnetic force

    Hello! The magnetic force is to the right. ##I_c## is the moment of inertia of the cylinder. For the net force on the centre of mass, I have the frictional and magnetic forces ##F=F_B-f##. I know that ##F_B## is ##IdB##. I also know that ##rf=I_c\alpha=I_c\frac ar##, so that...
  14. E

    Is this formula for a ball rolling down a ramp incorrect?

    I've got to do an experiment that essentially involves rolling a ball bearing down a (frictional) ramp and measuring its acceleration. It's quoted in the manual that the linear acceleration of a ball bearing rolling down a ramp at angle ##\theta## is ##a = \frac{5}{9} g \sin{\theta}##. When I...
  15. haushofer

    Rolling resistance when speed is zero

    Dear all, I have a very simple question. The rolling resistance (rr) of, say, a car, is defined as being proportional to the normal force/weight of an object. That seems reasonable: ##F_{rr} = C_{rr} \times F_N## The coefficient C_{rr} is a constant, depending on the materials. But now a...
  16. G

    The velocity of the center of the base of a rolling cone

    Let the vertex of the cone be ##O##, the contact point on the cone all the way to the right be ##D## touching ground. Then ##v_{\text{D relative to the table}} = v_{D/table} =0## since it rolls without slipping. Due to relative motion $$\vec v_{P/table} = \vec v_{P/D} + \vec v_{D/table} = \vec...
  17. aspodkfpo

    What is the relationship between torque, linear force, and rolling resistance?

    Say that I have a round object on a table and it is still. If I apply a force and it doesn't move the resistive force is rolling resistance rather than a frictional force right? Now I must be able to apply forces in different amounts until it exceeds a boundary for the object to move similar to...
  18. E

    A polygon is rolling down a hill

    An ##n##-sided regular polygon is rolling down a frictional ramp at angle ##\theta## to the horizontal. I define ##\beta := \frac{2\pi}{n}## as the angle at the top of each of the ##n## isosceles triangles that make up the polygon. Let ##\omega_{k, 1}## be the angular velocity just after the...
  19. Vivek98phyboy

    What am I Missing? Solving Conservation of Energy

    By solving conservation of energy, I was able to find the linear velocity which is [10g(H-R-Rsin(theta))/7]^½ and by differentiating this with respect to "t", I arrived at the tangential acceleration value of -(5gcos(theta))/7 and found it to be in agreement with the solution provided in the...
  20. E

    Ball rolling in a magnetic field

    I first found the Lorentz force on the ball as a whole$$\vec{F}_m = \iiint_V \rho(\omega \times \vec{r} + \vec{V})\times \vec{B} dV = \rho \vec{\omega} \times \left( \iint_V \vec{r} dV \right) \times \vec{B} + \rho \iiint_V \vec{V} \times \vec{B} dV = Q\vec{V} \times \vec{B}$$due to the...
  21. e2m2a

    Does Rolling Resistance Change with Speed on Polyurethane Wheels?

    I have conducted an experiment which involves measurements of the velocities of a carriage moving in a straight line which has 4 polyurethane caster wheels attached to it. (The kind you can get a hardware store.) In one phase of the test the carriage is pushed at about .1 meters per second. In...
  22. L

    Rolling with slipping and combined momentums

    Summary:: combining angular and linear momentum when an impulse is aplied 2/3 of the radius from the center. A Jo-jo is lying on the ground on its edge. The central part (axel) has a radius of 2r and it’s side a radius of 3r. The string is protruding from the bottom of the axel (central part)...
  23. LCSphysicist

    Cylinder rolling without slipping on a truck

    I don't know how to start it Is the truck who make the cylinder roll, initially? If yes, how? Since the truck force would pass by the center of the cylinder.
  24. LCSphysicist

    Solid disk rolling down an inclined plane -- Some conceptual questions

    I was always a little confused about the rolling down of a body, let's say, a sphere. It's know that to body rotate, from the rest, in a referential frame on the ground [inertial], is necessary a friction, that will just act like a medium that transforms kinetic energy of translation into...
  25. Serhatakguc0

    Dynamics homework -- Motion of a stick attached to a rolling disk

    Hi everyone, I need help for this homework. I'm a mechatronics engineering student and i want to solve this question but no matter how hard I try, I can't solve the question. Sorry for my bad english...The disk connected to the AB stick with a length of 2 meters is rolled as shown in the figure...
  26. Tony Hau

    Problem about a ball rolling on a rotating hoop

    [No template as this thread was moved to the homework forums after it had attracted several replies] Here I have a tutorial problem as follows: The problem I have is about part a, whose answer is as follows: When I solve the partial derivative on Vf w.r.t. r, I get Vf = mω^2rsin^2(θ)/2...
  27. ZD_zainy

    Angular velocity of a rolling object

  28. G

    Confusion on the concept of point of rotation

    --no explanation as conceptual error--
  29. Bilbo B

    How Does Roughness Affect the Time Period of a Ball Rolling on a Vertical Hoop?

    If the ball's rolling on a vertical hoop placed in contact with floor and with the lowest point being the mean position of the ball undergoing to and fro motion with small angular displacement. In what ways it's time period is solved out provided the surface of the hoop is rough. If the block is...
  30. SilverSoldier

    Mathematically Modeling a Rolling Body with Slipping

    Basically, I want to know if my assumptions and workings are correct. This is how I see this situation. First, I'm viewing this body as a series of disconnected points, like I have in this animation I made, modeling purely rolling motion. Modeling the body like that worked in that case, and...
  31. Leo Liu

    Cylinder Rolling Down an Incline Without Slipping

    First we let the static friction coefficient of a solid cylinder (rigid) be ##\mu_s## (large) and the cylinder roll down the incline (rigid) without slipping as shown below, where f is the friction force: In this case, ##mg\sin(\theta)## is less than ##F_{max}##, where ##F_{CM,max}## is the...
  32. U

    Why is rolling easier than sliding?

    I learned that rolling involves the coefficient of static friction unlike sliding that involves the coefficient of kinetic friction. It's known that the coefficient of static friction is always higher than the coefficient of kinetic friction. This should result in rolling to be more difficult...
  33. caesium

    Centripetal force for off-centered cylinders rolling down a curve

    My initial attempt: Total Centripetal force on the cylinder would be given by $$\textbf{F}_{net} = mR\omega^2 \textbf{e}_1+mr_{cm}\omega^2 \textbf{e}_2$$ where the vectors e_1 and e_2 have magnitude 1 and point radially outwards (and continuously changing as the cylinder rolls down) as marked in...
  34. IamVector

    Cylinder rolling with a block inside it

  35. M

    Kinetic energy of a disk that is rolling and not slipping

    Let ##\Theta## be the angle, following the movement of the center of the disk. In order to find the kinetic energy, we brake the movement of the disk into 2: The translation of the center of mass, and the rotation of the disk around it. So, the kinetic energy will be given by: $$T= \frac 1 2...
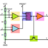
  36. Alexanddros81

    Vector Mechanics — Double Gear Rolling on a Rack

    Hi! My first question: How does he get the equation ##\frac {x_A} {2πr_1} = -\frac {θ} {2π}## ?
  37. Addez123

    B Probability of rolling a "6" k times out of 20 rolls of a die

    The probability should be ## (1/6)^k * (5/6)^{20-k} ## But the book says the answer is : ## \begin{pmatrix} 20 \\ k \\ \end{pmatrix} * (1/6)^k * (5/6)^{20-k} ## Because there are 20 over k different sequences, but the order doesn't matter? I just don't understand why the 20 over k is there...
  38. S

    3d simulation of a rolling ball

    How did you find PF?: Google Hi, I'm looking for advice on how to simulate a golf ball rolling on a green. The green will have been scanned using a 3d scanner by an Engineering Surveyor. I'm trying to model putting a golf ball from any position on the green, looking for a path line to the...
  39. kaloyan

    Kinetic energy of a ball rolling down a ramp

    Consider the situation in the attached photo. The kinetic energy in A is 10 J, in B is 30 J. What is the kinetic energy in C? Using that the mechanical energy is the sum of potential energy ##(E_p=mgh)## and kinetic energy ##(E_k=\dfrac{mv^2}{2})##, we get that the mechanical energies in...
  40. L

    Rolling without Slipping - axes of rotation and centripital acceleration

    Therefore, if someone were to ask what the magnitude of centripetal acceleration is at the top of the wheel at a given instant (relative to the ground): ##v_{cm} = v_{translational, center-of-mass/wheel}## ##ω = ω_{point-of-contact}## ##v_{top} = 2(v_{cm}) = 2(rω)## ##a_{c(top)} =...
  41. F

    Rolling friction and static friction....

    Hello, Static friction implies no relative (maybe just instantaneously) motion between the two objects that are in contact. Rolling friction pertains to rolling objects and develops due to the asymmetric deformation of the surface over which the body rolls (if the deformation was symmetric, the...
  42. A

    Kinematics without rolling or sliding

    I initially thought it is v, because the speed shouldn't change when the tape is on top.
  43. Automatic Strike Bowling Ball

    Automatic Strike Bowling Ball

    You don't need to be good at bowling if you're good at engineering.
    • Swamp Thing
    • Media item
    • arduino bowling robotics rolling
    • Comments: 0
    • Category: Pop Science
  44. anonymous99

    Rotational motion question -- Wire wound around a rolling spool

    Shouldn't the answer have the same magnitude regardless of sign convention?
  45. L

    Wheel Rolling Motion: Understanding Mgsin(θ) vs. fs-max

    Halliday's book says the following about a wheel rolling down a ramp: "Note that the pull by the gravitational force causes the body to come down the ramp, but it is the frictional force that causes the body to rotate and thus roll. If you eliminate the friction (by, say, making the ramp slick...
  46. D

    Rolling without slipping down an inclined plane

    Hi If a rigid disc rolls down an incline plane without slipping then the component of weight down the plane causes the disc to accelerate downwards but the frictional force causes a torque which causes the disc to rotate, At the point of rolling without slipping the velocity of the centre of...
  47. D

    Is My Calculation of a Rolling Steel Hoop's Acceleration Correct?

    I already have the answer but it doesn't make sense. For starters I think the question is worded badly. I think there are 2 different accelerations here ? The acceleration of the centre of mass and the acceleration due to rotation. I think the acceleration due to rotation doesn't affect the...
  48. Addez123

    Smooth rolling ball rolls down hill, how far can it fly?

    Figure of the problem. There are many exercises like these, and I've read the whole chapter and I got no clue where to start here. Kinetic energy from gravity is: E = mgh = 39.3m I could try change v to ωr in the K equation but it will leave me nowhere because I don't have the mass nor the...
  49. cs44167

    What is the coefficient of friction for a pen rolling down a book?

    I tried using coefficient of friction = friction / Normal force, but needed a value for friction. I then tried to find the friction using a = f/m, but was unsure of which value to plug in for force. Simply finding the force given a and m will not yield the correct answer; the net force must be a...
  50. jisbon

    Rotating cylinder rolling without slipping in a B field

    Firstly, I need to determine what the electric field is causing. Using left hand rule, the force due to the field is acting down the slope. Hence my FBD looks like: Where the two arrows pointing towards the right represent the force due to the field and weight of the cylinder. Since ...
Back
Top