Spacetime interval Definition and 52 Threads

In physics, spacetime is any mathematical model which fuses the three dimensions of space and the one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur.
Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. The famous physicist Albert Einstein helped develop the idea of space-time as part of his theory of relativity. Prior to his pioneering work, scientists had two separate theories to explain physical phenomena: Isaac Newton's laws of physics described the motion of massive objects, while James Clerk Maxwell's electromagnetic models explained the properties of light. However, in 1905, Albert Einstein based a work on special relativity on two postulates:

The laws of physics are invariant (i.e., identical) in all inertial systems (i.e., non-accelerating frames of reference)
The speed of light in a vacuum is the same for all observers, regardless of the motion of the light source.The logical consequence of taking these postulates together is the inseparable joining together of the four dimensions—hitherto assumed as independent—of space and time. Many counterintuitive consequences emerge: in addition to being independent of the motion of the light source, the speed of light is constant regardless of the frame of reference in which it is measured; the distances and even temporal ordering of pairs of events change when measured in different inertial frames of reference (this is the relativity of simultaneity); and the linear additivity of velocities no longer holds true.
Einstein framed his theory in terms of kinematics (the study of moving bodies). His theory was an advance over Lorentz's 1904 theory of electromagnetic phenomena and Poincaré's electrodynamic theory. Although these theories included equations identical to those that Einstein introduced (i.e., the Lorentz transformation), they were essentially ad hoc models proposed to explain the results of various experiments—including the famous Michelson–Morley interferometer experiment—that were extremely difficult to fit into existing paradigms.
In 1908, Hermann Minkowski—once one of the math professors of a young Einstein in Zürich—presented a geometric interpretation of special relativity that fused time and the three spatial dimensions of space into a single four-dimensional continuum now known as Minkowski space. A key feature of this interpretation is the formal definition of the spacetime interval. Although measurements of distance and time between events differ for measurements made in different reference frames, the spacetime interval is independent of the inertial frame of reference in which they are recorded.Minkowski's geometric interpretation of relativity was to prove vital to Einstein's development of his 1915 general theory of relativity, wherein he showed how mass and energy curve flat spacetime into a pseudo-Riemannian manifold.

View More On Wikipedia.org
Recent contents Top users
  1. Sciencemaster

    I Series Expansion of the Infinitesimal Spacetime Interval

    I was watching an explanation of why the spacetime interval is invariant in all inertial frames (even when it's not lightlike) and the author made the assertion that if we have the relationship ds'=f(ds), we can expand the function as A+B*ds+C*ds^2+... (where C is not the speed of light). That's...
  2. cianfa72

    I SR flat Lorentzian manifold and Anderson simultaneity convention

    Hi, I was thinking about the following. From a mathematical point of view, SR assumes the following postulate: spacetime is a flat Lorentzian smooth manifold. From the above and a minimal interpretation (i.e. a minimal set of "rules" to define the correspondence between mathematical objects...
  3. C

    B Spacetime interval question involving a Pendulum in a Space Ship

    Hello everyone, I was working on a thought experiment and came upon an inconsistent result that I thought maybe I could get some help with. Firstly I am using natural units (c = unitless 1 i.e 1 light second per second) and I chose v = 3/5 to make gamma come out nicely (gamma equals 5/4 when v...
  4. S

    I Need to resort to spherical wavefront to derive the LTs?

    I have been reading Wikipedia’s derivations of the Lorentz Transformations. Many of them start with the equation of a spherical wavefront and this reasoning: - We are asked to imagine two events: light is emitted at 1 and absorbed somewhere else at 2. For a given reference frame, the distance...
  5. H

    I Spacetime interval and basic properties of light

    While not having a professional physics background I was still interested in knowing more about special and general relativity. Therefore I was trying to find out where the space time interval was coming from in relation to the speed of light. Of course this is the first point to start I...
  6. LCSphysicist

    Special relativity - Trivial exercise with spacetime interval

    For a observer on Earth, a rocket takes Mike from Earth to Pluto with a speed of 0.82 c for 33.72 yr. Find the space-time interval for the two events such as Mike leaving the Earth and reaching Pluto considering Pluto is at rest relative to Earth for the observer on Earth. I confess that i am...
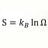
  7. morrobay

    B Time like spacetime interval, proper time, and time dilation

    Since the time like spacetime interval is equal to proper time for stationary or traveling observers, then it seems time dilation (proper time) seen with traveling clock is necessarily frame invariant. Then the so called time between ticks of both identical clocks, with stationary and traveling...
  8. Kaguro

    Deriving length contraction using spacetime

    Deriving time dilation was easy: Imagine two events in frame O' at the same location. ##ds^2 = -c^2 dt'^2## The same viewed in O frame is: ##ds^2 = dx^2+dy^2 + dz^2 - c^2 dt^2## ##\Rightarrow dx^2+dy^2 + dz^2 - c^2 dt^2 = -c^2 dt'^2## ##\Rightarrow (\frac{dx}{dt})^2+(\frac{dy}{dt})^2+...
  9. greg_rack

    B Definition of Spacetime Interval

    Hi guys, I'll attach an excerpt from my textbook which isn't, in my opinion, very clear in explaining a spacetime interval(or I'm just missing the key to get the concept). "How do we combine two different measurements such as time and space, to form an invariant variable? We can simply write...
  10. cianfa72

    I The spacetime length of finite spacelike intervals

    Hello, I'm aware of the following topic has already been discussed here on PF, nevertheless I would like to go deep into the concept of "finite spacelike interval" in the context of SR and GR. All us know the physical meaning of timelike paths: basically they are paths followed through...
  11. G

    I Exploring Spacetime Interval at a Singularity: Tad Williams' Otherland

    Tad Williams’ Otherland series has a scene where the characters are drawn to a temple no matter which direction they try to walk, as if space itself is curved. This is kind of the intuition I get when a physicist talks about the spacetime interval kind of flipping past an event horizon: if you...
  12. MattGeo

    I Spacetime Interval & Energy-Momentum 4Vec: Reconciling Hyperbolic Geometry

    In a spacetime diagram the spatialized time direction is the vertical y-axis and the pure space direction is the horizontal x-axis, ct and x, respectively. The faster you go and therefore the more kinetic energy you have, you'll have a greater component of your spacetime vector in the...
  13. benorin

    B SR Thought: Spacetime Interval w/ Bounds of ##0<\alpha<1##

    Suppose the time interval in the Lab frame is a multiple of the time interval in the Rocket frame ##\alpha \Delta t_L = \Delta t_R##, where ##0 < \alpha < 1## without loss of generality. Then the spacetime interval is ##\left( \Delta t_L\right) ^2-\left( \Delta x_L\right) ^2 = \left( \Delta...
  14. L

    Differentiating with coordinate transformations

    T = (x+\frac{1}{\alpha}) sinh(\alpha t) X = (x+\frac{1}{\alpha}) cosh(\alpha t) - \frac{1}{\alpha} Objective is to show that ds^2 = -(1 +\alpha x)^2 dt^2 + dx^2 via finding dT and dX and inserting them into ds^2 = -dT^2 + dX^2 Incorrect attempt #1: dT= (dx+\frac{1}{\alpha})...
  15. S

    I Applying the spacetime interval to regular vectors instead of curves

    I have some questions. Let us assume for these questions that I am using the (- + + +) sign convention. Firstly, we know that if you have a parameterized curve ξ(s), then you can find the proper time between two events at points s1 and s2 by using this formula (assuming that the curve is...
  16. W

    B Spacetime interval - alternative view - maybe?

    With regard to special relativity… Whenever, I come across the spacetime interval, written like this, say, (Δs)2 = (Δt)2 – (Δx)2 – (Δy)2 – (Δz)2 , it is as if it has to be that way. However, it seems to me it is this way by definition and does not have to be so. Sometimes, it seems to be...
  17. Prez Cannady

    I Inhomogeneous Wave Eq. & Minkowski Spacetime Interval

    Answer is probably not, but is there some connection between the inhomogeneous wave equation with a constant term and the spacetime interval in Minkowski space? $$ 1) ~~ \nabla^2 u - \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} = \sum_{i=0}^2 \frac{\partial^2 u}{\partial x_i^2} -...
  18. nomadreid

    I What is the Term for ds in Spacetime Interval Equation?

    In the usual relativistic equation, ds2 = (cdt)2 - dx2 - dy 2 -dz2 or dx2 + dy 2 + dz2 - (cdt)2, depending on the convention of your choice, and ds2 is called the spacetime interval between the corresponding events, the square being used to avoid nasty ambiguities and irritating imaginary...
  19. haushofer

    I Gravitational time dilation, proper time and spacetime interval

    Dear all, I'm having confusion about the standard derivation of Schwarzschild's gravitational time dilation. For concreteness I'll follow the explanation of Schutz' "gravity from the ground up", but other texts argue the same. So let me rephrase Schutz's explanation (I surpress factors of c in...
  20. F

    I Why is proper time undefined for spacelike/lightlike paths?

    As I understand it, the proper time, ##\tau##, between to events in spacetime is defined in terms of the spacetime interval ##ds^{2}=\eta_{\mu\nu}dx^{\mu}dx^{\nu}##, such that $$d\tau =\sqrt{-ds^{2}}$$ (where we are using the "mostly +" signature with ##c=1##). Now, for time-like intervals, for...
  21. J

    I On the invariant speed of light being the upper speed limit

    Hello! I have a question that has been bothering me since I first started learning about Special Relativity: Given only the Minskowskian metric and/OR the spacetime interval, how can one reach the conclusion that the speed of light is invariant for every observer and how can one conclude that it...
  22. F

    I Parametrisation of timelike curves using proper time

    Apologies if this is a really stupid question, but what is the exact argument for why one can use proper time to parametrise timelike curves? Is it simply that the arclength of a timelike curve is its elapsed proper time and hence we are simply parametrising the curve by its arclength? Also, is...
  23. D

    Consequences of space-/time-/light-like separations

    I'm trying to prove the following statements relating to space-like, time-like and light-like space-time intervals: 1. There exists a reference frame in which two space-time events are simultaneous if and only if the two events are space-like separated. 2. There exists a reference frame in...
  24. D

    Coincidence of spacetime events & frame independence

    I have been reading these notes: http://isites.harvard.edu/fs/docs/icb.topic455971.files/l10.pdf in which they claim that if two spacetime events are coincident in one frame of reference then they are coincident in all inertial frames of reference, thus spacetime events are absolute i.e. they...
  25. D

    Simultaneous events, space-like separation & QFT

    First of all, sorry if this is in the wrong forum, wasn't quite sure which one to post it in given the question. My question is, given two space-time points ##x^{\mu}## and ##y^{\mu}##, if the events that occur at these points are simultaneous, i.e. ##x^{0}=y^{0}##, are the two events...
  26. R

    Measuring Relative Speed of Frames Using Spacetime Interval

    Hi all, Say two events happen in the same place according to one observer (1). They are separated in time by 3 years. According to another observer (2) that is moving relative to the first, the events are separated by 5 years. We can calculate, using the invariance of the spacetime interval...
  27. fezster

    Connection between Lorentz covariance and special relativity

    s2 = t2 - x2 - y2 - z2 This equation is covariant (Lorentz covariance). The interval "s" is invariant (Lorentz invariance). Can you derive everything in special relativity from these facts? Or am I mistaken about that?
  28. N

    Light like interval in wave function

    I have read the following from what seems a reliable source: The identification of the spacetime interval with quantum phase applies to null intervals as well, consistent with the fact that the quantum phase of a photon does not advance at all between its emission and absorption. Hence the...
  29. J

    Spacetime Interval & Metric: Equivalent?

    This may seem an odd question but it will clear something up for me. Are "The spacetime interval is invariant." and the "The spacetime metric is a tensor." exactly equivalent statements? Does one imply more or less information than the other? Thanks!
  30. C

    Relativity & Spacetime: Interval Explained

    Hi! I'm a student reading a book given to me by my teacher about relativity and spacetime. It says that the separation between events in spacetime is measured in "intervals," and I can understand that part. What I don't understand is why you subtract the squares of the distance in space instead...
  31. A

    Invariant Spacetime Interval for Classical Spacetime

    In special relativity we have the invariant spacetime interval ds2 = dx2 - c2dt2. If we think about classical (non-relativistic) space and time as one spacetime in which the transformation between reference frames is given by the Galilean transformation, is there a corresponding spacetime...
  32. P

    Why is there a Minus in Spacetime Interval Formula?

    Hello everyone Please help me understand why there is a minus in the spacetime interval formula and not a plus Thanks in advance
  33. C

    Why does observers agree on the spacetime interval?

    Since two observers with coinciding origins at t=t'=0 both measures a light wave to be moving at c they will both claim that r^2= (ct)^2 and thus that r^2-(ct)^2 = 0. Thus r'^2 - (ct)^2 = r^2 - (ct)^2 = 0 which is really just stating that 0=0 for events following the spherical wave off...
  34. M

    Calculating Spacetime Interval for Event A

    Homework Statement The spacetime interval between the origin in frame S and an event, A, is found to be r = 8 lightseconds. In frame S' moving in Standard orientation with respect to S at speed v = 0.5c event A is measured at a distance r' = 6 lightseconds from the origin. (a) What is...
  35. C

    (Re-Answered) Spacetime interval homework question?

    (This problem was previously asked but poorly answered. Here is a link to the previous locked thread. https://www.physicsforums.com/showthread.php?t=202855) 1. State the problem, all variables and given/known data The star Alpha goes supernova. Ten years later and 100 ly away, as measured by...
  36. T

    Spacetime Interval in non-inertial frames.

    The interval between two events ds^2 = -(cdt)^2 + x^2 + y^2 + z^2 is invariant in inertial frames. I was wondering, if this same interval still applies and is invariant in non-inertial frames?
  37. S

    How Do You Calculate Spacetime Intervals for a Merry-Go-Round Ride?

    Homework Statement Two friends with super-synchronized clocks. One goes on merry-go-round the other stands outside at the same point. The merry-go-round has a constant v of 45 m/s and takes 300s to go around. Find dt, ds, and dτ. Homework Equations v=dx/dt v=2πR/p using...
  38. G

    How does gravitational time dilation increase the spacetime interval?

    I (think I) understand that: 1. With the Schwarzschild metric, the ratio of proper time to coordinate time decreases ("clock runs slower") with decreasing radial distance. (And ratio of proper distance to coordinate distance increases.) 2. The geodesic path followed by a freely falling...
  39. K

    Spacetime Interval: Is it Invariant Under Rotations?

    I know that the spacetime interval is the same in coordinate system moving wrt each other at constant speed. But is it true that the spacetime interval is invariant under rotations? If so can you suggest a proof or post a link to one?
  40. P

    Spacetime Interval Relativity question.

    Homework Statement Two events occur 5 s apart in time and 3 s apart in space. A clock traveling at a speed of .6 can be present at both these events. What time interval will such a clock measure between the events? A. 8 s B. 5.8 s C. 5 s D. 4 s E. 2 s F. Other Homework Equations...
  41. M

    Invariance of spacetime interval

    I've tried proving the invariance of the spacetime interval from Lorentz transformations 3 times now, but every time I end up with two extra terms that don't cancel! Could I have some help?
  42. S

    Space-Time Interval: Exploring Schutz's Explanation

    I have been working through Schutz's A First Course in General Relativity and was a little confused by how he presents the space time interval: \Delta \overline{s}^2 = \sum_{\alpha = 0}^{3} \sum_{\beta = 0}^{3} M_{\alpha \beta} (\Delta x^{\alpha})(\Delta x^{\beta}) for some...
  43. E

    Simple spacetime interval question

    Homework Statement on a spacetime plot (y-axis) = t (x-axis) = x find the spacetime interval between points (0,0) and (300,700) Homework Equations Interval = (c^2(del t)^2 - (del r)^2)^1/2 The Attempt at a Solution So I can see clearly my del t is 700 (700 - 0 = 700 ) but for the...
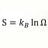
  44. morrobay

    Less elapsed time: Lorentz Transformation or Spacetime Interval ?

    With one clock stationary at the common origin for 10 time units and the other rocket clock traveling out and back at v=.6c. When both clocks are compared at the origin the elapsed time on the traveling clock will show less time by a factor of (.8) from the Lorentz Transformation. The...
  45. T

    Understanding the Spacetime Interval and the Condition for Simultaneity

    The spacetime interval s between two events is s^2 = c^2*t^2 - x^2 where t is the time between the 2 events and x is the distance between the 2 events in a given frame of reference. What is the general condition on s such that two events cannot be simultaneous in any frame? I don't...
  46. 2

    Calculating Spacetime Interval: Alpha & Beta Supernovae

    Homework Statement The star Alpha goes supernova. Ten years later and 100 ly away, as measured by astronomers in the galaxy, star Beta explodes. An alien spacecraft passing through the galaxy finds that the distance between the two explosions is 120 ly. According to the aliens, what is the...
  47. K

    Is the Spacetime Interval Truly Invariant Across Different Reference Frames?

    I am working on a homework problem, and because it is a homework problem, I will not tell you the specifics or ask for an answer. My question has very little to do with the problem in particular, I just wanted to make that disclaimer. Oh, and the derivation of the Lorentz transformation was NOT...
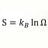
  48. morrobay

    What does a spacetime interval of zero mean for objects traveling at c?

    When an object is traveling at c the spacetime interval is zero. I can follow the algebra that gets to this conclusion. Is there a conceptual, mentally conceived image, explanation for a spacetime interval of zero ?
  49. J

    How Do You Calculate Time Difference in Different Inertial Systems?

    Homework Statement Two events occur in an inertial system at the same time, but 9000 km apart. However in another inertial system these two events are observed to be 11000 km apart. What is the time difference between the two events in this second inertial system? Homework Equations...
  50. N

    What is the dimension of the spacetime interval?

    Just what the title says. In the book Spacetime Physics, by Taylor and Wheeler, the time coordinate is measured in metres of light-travel time, but that's just a roundabout way of saying that they are using the second...or am I missing the point. :blushing:
Back
Top