You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
States Definition and 1000 Threads
-

XYZ spectroscopy and the existence of possible 4-quark states
Hi everyone, I've been studying the so-called XYZ spectroscopy and the existence of possible 4-quark states. The LHCb collaboration recently confirmed the existence of a particle called Z(4430)^-. This particle is the unambiguous evidence for the existence of 4-quark states. From what I...- Einj
- Thread
-
- Tags
- Existence Spectroscopy States
- Replies: 8
- Forum: High Energy, Nuclear, Particle Physics
-
U
Harmonic Oscillator, overlap in states
Homework Statement Particle originally sits in ground state about x=0. Equilibrium is suddenly shifted to x=s. Find probability of particle being in new first excited state. Homework Equations The Attempt at a Solution Shifted wavefunctions are for ground state: ##\phi'_0 =...- unscientific
- Thread
- Replies: 5
- Forum: Advanced Physics Homework Help
-
U
How does the density of states change with temperature?
Homework Statement Part (a): Plot fermi energy as a function of N Part (b): Derive the density of states and find its value Part (c): How many atoms reside at 20% of fermi energy? Estimate diameter of cloud Part (d): For the same atoms without spin, why is the cloud much smaller...- unscientific
- Thread
- Replies: 5
- Forum: Advanced Physics Homework Help
-
G
Bound States, Negative Potential, Alternate Basis, Matrix Mechanics
Homework Statement Given the potential V(x) = - 1/ sqrt(1+x^2) Consider this in a 50x50 matrix representation of the hamiltonian in the basis of a one dimensional harmonic oscillator. Determine the eigenvalues and eigenvecotrs, the optimal parameter for the basis, and cop ate the...- GeneralGrant
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-
A
Understanding CMOS Gate States: Shoot-Through and Capacitance Effects
Please help me with the question in the picture about pull-up and pull-down networks. -
H
Interpretation verification: Partition function vs. number of states
Greetings, I have been studying stat mech lately, and while I have gotten good at using partition functions to solve problems, I wanted to check my interpretation of what a partition function is, and especially to contrast it with the number of states. So, I'm just looking for a yes or no to...- HJ Farnsworth
- Thread
- Replies: 2
- Forum: Classical Physics
-
C
Physically realisable states and spectra
We've been assigned Griffiths QM for undergraduate physics. I don't particularly like it, but anyway. It says that if the eigenvalues an observable are continuous then the eigenfunctions do not represent physically realisable states. So the eigenfunctions of the hamiltonian are discrete and...- cooev769
- Thread
- Replies: 6
- Forum: Quantum Physics
-
U
Transition between two states probability
Homework Statement Part (a): Show probability to transit from state i to j is given by: Part (b)i: Use answer in part (a) to find probability Part (b)ii: Use time evolution to find probability Homework Equations The Attempt at a Solution Part (a) was alright, bookwork question on time...- unscientific
- Thread
-
- Tags
- Probability States Transition
- Replies: 13
- Forum: Advanced Physics Homework Help
-

Quantum Mechanics - Time evolution operator , bra ket states.
The question is to calculate the time evoution of S_{x} wrt <\Psi(t)\pm l where <\Psi\pm (t) l= ( \frac{1}{\sqrt{2}}(exp(^{+iwt})< \uparrow l , \pm exp(^{-iwt})< \downarrow l ) [1] Sx=\frac{}{2}(^{0}_{1}^{1}_{0} ) Here is my attempt: - First of all from [1] I see that l \Psi\pm (t) > = (...- binbagsss
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Determining the states in Markov chains
Homework Statement This is not a homework question, just me trying to wrap my head around things. My probability class talked about Markov chains for less than 2 hours worth of lecture, and I've been super sick lately, so I'm still a little confused. If we're considering real world...- stripes
- Thread
-
- Tags
- States
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
Solving Matrix Eigenvalue Equation for ψ_{200} and ψ_{210} States
In order to apply perturbation theory to the ψ_{200} and ψ_{210} states, we have to solve the matrix eigenvalue equation. Ux=λx where U is the matrix of the matrix elements of H_{1}= eEz between these states. Please see the matrix in attachment 1. where <2,0,0|z|2,1,0>=<2,1,0|z|2,0,0>=3a_{o}...- M. next
- Thread
-
- Tags
- Eigenvalue Matrix States
- Replies: 1
- Forum: Quantum Physics
-
M
Probability of 5 Spin 1/2 Particles in No Magnetic Field
Homework Statement Consider an ideal system of 5 non-interacting spin 1/2 particles in the absence of an external magnetic field. What is the probability that n of the five spins have spin up for each of the cases n = 0, 1, 2, 3, 4, 5? Homework Equations I'm guessing \frac{N!}{n!(N-n)!}...- moknight
- Thread
-
- Tags
- Probability States
- Replies: 1
- Forum: Advanced Physics Homework Help
-
X
What is the Number of Spin s States for Two Identical Particles?
Number of Spin "s" States Homework Statement For a system of two identical particles with spin s, determine the number of symmetric and anti-symmetric spin states. 2. The attempt at a solution This does not seem like a problem that is that difficult, but I am having some trouble...- Xyius
- Thread
- Replies: 8
- Forum: Advanced Physics Homework Help
-
U
Delta Potential - Bound and Continuum States
Homework Statement I am studying my lecturer's notes and in this part he uses a delta potential to illustrate a simple example of Fermi's golden rule, that the rate of excitation is ##\propto t##. Homework Equations The Attempt at a Solution I've managed to get the bound states, by solving...- unscientific
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-
K
Why are exited states of an Isotope metastable?
Why are exited states of an Isotope metastable? Is it because they have a large spin and therefore the final states they decay to have to be excited as well? And therefore they have less energy gain? I am thinking about 116 In (the 1+ and 5+ state) both can undergo a β- decay. Thank you!- kuecken
- Thread
- Replies: 4
- Forum: High Energy, Nuclear, Particle Physics
-
K
Atomic Energy States in a Crystal: Einstein's Relation
Does atoms in a crystal have energy states like electronic states? it is according to Einstein relation for harmonic oscillator.E=nhw- kur82
- Thread
- Replies: 1
- Forum: Atomic and Condensed Matter
-
J
How Do You Calculate the Density of States for Massless Particles in a 3D Cube?
Homework Statement Calculate the single particle density of states for massless particles with dispersion E=h_bar ck for a 3D cube of volume V Homework Equations E=pc, p=E/c, dp=dE/c, d^3p = 4pi*p^2 dp k=sqrt(k_x^2+k_y^2+k_z^2) k_j = 2pi/L l_j (j=x,y,z) The Attempt at a Solution I...- jammydav93
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-

States are or aren't unit vectors?
I am a little confused by an elementary point. Something must be wrong with the following: On one hand, a Hermitian operator (which is not necessarily unitary) takes one state to another state. Hence a state need not be represented as a unit vector; its norm can be greater (or less than)...- nomadreid
- Thread
-
- Tags
- States Unit Unit vectors Vectors
- Replies: 16
- Forum: Quantum Physics
-
M
Can there be multiple ground states?
I am reading an article on wikipedia about ground state and it says - The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the...- marc32123
- Thread
- Replies: 1
- Forum: Other Physics Topics
-
L
Why massless particle can only have two helicity states?
why massless particle, such as photon, can only have two helicity states? Photon's helicity is 1,-1. Helicity zero is forbidden. why? -
M
Q value with species in different states
Given the half reaction: 2H2O(l) → O2(g) + 4H+(aq) + 4e- How would you set up the Q equation for this reactions? Would it be Q = [H+]4 only or do we assume the partial pressure of oxygen gas is 1 atm? Is there a general way to write the Q value for species in different states? -
R
Mathematical Biology (steady states)
non-dimensionalisation equation: \begin{equation} \frac {du}{d\tau}=\frac{\overline{\lambda}_{1} u}{u+1} -\overline{r}_{ab}uv -\overline{d}u \end{equation} where $\overline{\lambda}_{1}= \frac {\lambda_{1}}{\lambda_{2} K_{1}}$ Another non-dimensionalisation equations \begin{equation} \frac...- ra_forever8
- Thread
-
- Tags
- Biology Mathematical States
- Replies: 1
- Forum: General Math
-

Exploring Mixed States: Preparation and Measurement
As mixed states and density matrices are the generalization of pure states, i wondered if it was possible to prepare a given mixed state. I know that decoherence give mixed states. Are there other ways to get them? measurements on pure states always give pure states (POVM also). So how?- naima
- Thread
- Replies: 17
- Forum: Quantum Physics
-

Energy required to cycle a counter through its states.
Greetings, While attempting to learn something about cryptography, I have repeatedly encountered a commonly quoted argument about the minimum energy required to cycle a 256 bit counter through all its states. It says that the absolute minimum energy required to change the state of a bit is... -
B
Help understanding molecular vs atomic electron quantum states
I am a retired electrical engineer, now able to get back to studying what I really enjoy - mathematics and physics. As a genuine old geezer, my modern physics knowledge, which was never very deep, is now way out of date. I purchased a copy of "Modern Physics", by Kenneth Krane, and have been...- Bob65
- Thread
- Replies: 5
- Forum: Quantum Physics
-
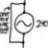
State Transition Matrix, Determining States
Homework Statement An LTI system is given in state-space form, \left( \begin{array}{cc} \dot{x_{1}} \\ \dot{x_{2}} \end{array} \right) = \left( \begin{array}{cc} -1 & 0.5 \\ 1 & 0 \end{array} \right) \left( \begin{array}{cc} x_{1} \\ x_{2} \end{array} \right) + \left( \begin{array}{cc} 0.5 \\...- jegues
- Thread
- Replies: 5
- Forum: Engineering and Comp Sci Homework Help
-
S
Exploring the Possibility of Deducing Quantum States from a Density Matrix
Is it not possible to deduce quantum states from a density matrix?- suma
- Thread
- Replies: 7
- Forum: Quantum Physics
-
G
Calculating Probability of Field States in QFT
Is it actually possible to calculate the probability of field states in QFT? For example the probability of some scalar field being found as some function f(x,t), i find this problem ignored in most texts.- GarageDweller
- Thread
-
- Tags
- Probability Qft States
- Replies: 8
- Forum: Quantum Physics
-
S
Exploring Photon States: Questions and Answers
I have few questions to ask: 1. Can a photon state be written as |ψ> = [cos(θ) sin(θ) exp(i*ø)] in column vector form 2. When a general photon state|ψ> = [cos(θ) sin(θ) exp(i*ø)] passes through a linear polarizer [1 0; 0 0] we get [cos(θ) 0] at the output but not [1 0] as is usually...- suma
- Thread
- Replies: 1
- Forum: Quantum Physics
-
G
'Largest' Schrodinger cat states created to date?
Hey, I've been searching around for papers reporting on the creation of relatively large cat states, the largest I have been able to find are by Wineland, and are on the scale of nano meters. Does anyone know of any articles where such states have been created (experimentally) and reported...- Gwinterz
- Thread
-
- Tags
- Schrödinger States
- Replies: 2
- Forum: Quantum Physics
-
K
Quantum States and ladder operator
In any textbooks I have seen, vacuum states are defined as: a |0>= 0 What is the difference between |0> and 0? Again, what happens when a+ act on |0> and 0? and Number Operator a+a act on |0> and 0?- kashokjayaram
- Thread
- Replies: 13
- Forum: Quantum Physics
-
S
Understanding Angular Momentum States and Clebsh-Gordan Coefficients
When we add the angular momenta of two particles, J1 and J2, we get that the resulting total angular momenta is in the range |J1-J2| < J < J1+J2 but according to the Clebsh-Gordan table some coefficients are zero. Does it mean that not all combinations between |J1-J2| and J1+J2 are possible?- spookyfish
- Thread
- Replies: 4
- Forum: Quantum Physics
-
0
Orthogonality of wave functions to negative momentum states
This is a question I have about the textbook discussion, so I'll do away with the standard format. The author of my QM book (Shankar, Principles of Quantum Mechanics) used the term "negative momentum states," all of a sudden, and I've never heard of it before. He has a little note saying that...- 0celo7
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Individual states of a particular energy level
In thermodynamics what is meant by "the number of individual states that belongs to one energy level"?My current understanding is that different individual states of one energy means a system with different pressure,volume and temperature that belongs to a particular energy level? please can...- abi.ayan
- Thread
-
- Tags
- Energy Energy level States
- Replies: 2
- Forum: Other Physics Topics
-
P
Double delta function and bound states.
Homework Statement Given the delta function -α[δ(x+a) + δ(x-a)] where α and a are real positive constants. How many bound states does it possess? Find allowed energies for \frac{hbar2}{ma} and \frac{hbar2}{4ma} and sketch the wave functions. Homework Equations I know there are three parts of...- petera88
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
B
Pure, proper mixed, and improper mixed states in laymen's terms
This is how one poster tried to explain it to me but for people who have only taken a basic physics course in college it leaves a lot wanting. "If a system is in a pure state, and you know what the pure state is, then your knowledge of the system is complete, and all uncertainty is quantum...- batmanandjoker
- Thread
- Replies: 12
- Forum: Quantum Physics
-
S
Question on Boltzman statistics and numbering of states
Consider a monatomic gas of hydrogen (just to make the example as simple as possible) at a temperature T. If I use Boltzmann statistics, I would say that the probability of finding any arbitrary atom at energy E should be proportional to ##g_i e^{-E_i/(k_BT)} / Z(T)## where ##g_i## is the...- Sonderval
- Thread
-
- Tags
- States Statistics
- Replies: 9
- Forum: Classical Physics
-
M
Solid-State and molecular physics; allowed energy states
When two objects move under the influence of their mutual force alone, we can treat the relative motion as a one-particle system of mass μ=m1m2/(m1+m2). An object of mass m2and charge -e orbits an object of mass m1 and charge +Ze. By appropriate substitutions into formulas given in the chapter...- mjmontgo
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Calculating Electron Density of States at Dirac Point in Graphene
Homework Statement Using the dispersion relation at the Dirac Point calculate the electron density of states for graphene in both the valence and conduction band. Homework Equations ρ = density of states = k2/pi2 The Attempt at a Solution I looked up what Dirac Points...- Aelo
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
N
Understanding BPS States and Their Relation to Supersymmetry Generators
A quick and simple question: one always talks about BPS states annihilating half the supercharges. What does that mean exactly? For example, in a pedagogical article by Alvarez-Gaumé and Hassan they give the anticommutator of one set of supercharges to be \{b_\alpha, b_\beta^\dagger \} =...- nrqed
- Thread
- Replies: 4
- Forum: Beyond the Standard Models
-
S
Question about Density of states
How can we define density of state in continuous energy? As the term energy state comes from quantum mechanics which deals with discrete energies. Thanks in advance- Shan K
- Thread
- Replies: 3
- Forum: Quantum Physics
-
H
Density of states for fermions and bosons
To take into account the density of states for an ideal gas, we first calculate it ignoring the spin. Then to take into account the spin for a system of electrons we put the number 2 for two spin directions. Why don't we do such this for a boson gas? For example if we have a gas of spin 1...- hokhani
- Thread
- Replies: 3
- Forum: Quantum Physics
-
J
E=mc^2 states mass and energy are interchangeable but ?
e=mc^2 states mass and energy are interchangeable but ?? But daltons law of constabt mass is voilated as states that while a reaction the mass of product = mass of reactant any explanations?- jagdishdash
- Thread
- Replies: 5
- Forum: Chemistry
-
D
A question re. 'single-particle' states
Hi, Seasons greetings to everyone :-) I've been revising statistical mechanics and have stumbled across an area that I've always been a little 'hazy' on. By the term 'single-particle' state, is it meant that this is a particular quantum state that one (or more) particle(s) can occupy, a...- "Don't panic!"
- Thread
-
- Tags
- States
- Replies: 6
- Forum: Quantum Physics
-
L
Graph States for Quantum Secret Sharing
In Graph States for Quantum Secret Sharing on page 3 : I understand that $$\mathop \otimes \limits_i Z_i^{{l_{i2}}} = Z_1^{{l_{12}}} \otimes Z_2^{{l_{22}}} \otimes Z_3^{{l_{32}}}$$ But I don’t understand why $$\left| G \right\rangle = \left( {\frac{{\left| {0 + + } \right\rangle +...- limarodessa
- Thread
- Replies: 1
- Forum: Quantum Physics
-
T
Molecular States, Symmetry and Allowed Transitions
I have a question about allowed transitions and molecular states. For an electric dipole transition between two states (say molecular or atomic) to have a non-zero probability of occurring, the transition dipole moment \langle \psi_{f}|\textbf{μ}\left|\psi_{i} \right \rangle must be non-zero...- tomothy
- Thread
- Replies: 1
- Forum: Quantum Physics
-
A
Kittel: possible states of magnetic
I do not understand the attached picture excerpt from Kittel Thermal Physics (first sentence up to 'eqn' (7) ). I would expect the moments to go down in increments of one, not two. I think the subsequent paragraph tries to explain why, although I am not sure this is indeed the purpose...- Aziza
- Thread
- Replies: 2
- Forum: Electromagnetism
-
L
Qubit system, time dependent states.
Homework Statement See attachment Homework Equations The Attempt at a Solution (i) |\Psi(t)_{1}>=e^{{-itE_{1}/\hbar}}\frac{1}{\sqrt{2}}(|z^{+}>+|z^{-}>) |\Psi(t)_{2}>=e^{{-itE_{2}/\hbar}}\frac{1}{\sqrt{2}}(|z^{+}>-|z^{-}>) where...- Lengalicious
- Thread
-
- Tags
- Qubit States System Time Time dependent
- Replies: 12
- Forum: Advanced Physics Homework Help
-
R
What Is the Coherent State for This EM Field?
\HugeHomework Statement Consider a state of the EM field which satisfies \left\langle \textbf{E}_x(\vec{r})\right\rangle =f(\vec{r}) Find a coherent state which satis es these expectation values.Homework Equations \textbf{E}(\textbf{r})=\frac{i}{\sqrt{2 V}}\sum _{\textbf{k},\lambda }...- Raz91
- Thread
- Replies: 5
- Forum: Advanced Physics Homework Help
-
H
What Is the Shortest Wavelength Photon an Electron Can Emit in a Quantum Trap?
Homework Statement There is a thin tube in which a finite potential trap has been set up where V2 = 0 V. An electron is shown traveling rightward toward the trap, in a region with a voltage of V1 = -9.00 V, where it has a kinetic energy of 2.00 eV. When the electron enters the trap region...- hvthvt
- Thread
-
- Tags
- Energy Energy states Quantum States
- Replies: 1
- Forum: Introductory Physics Homework Help