About the constraint equations of a pulley

[nish95]

Homework Statement

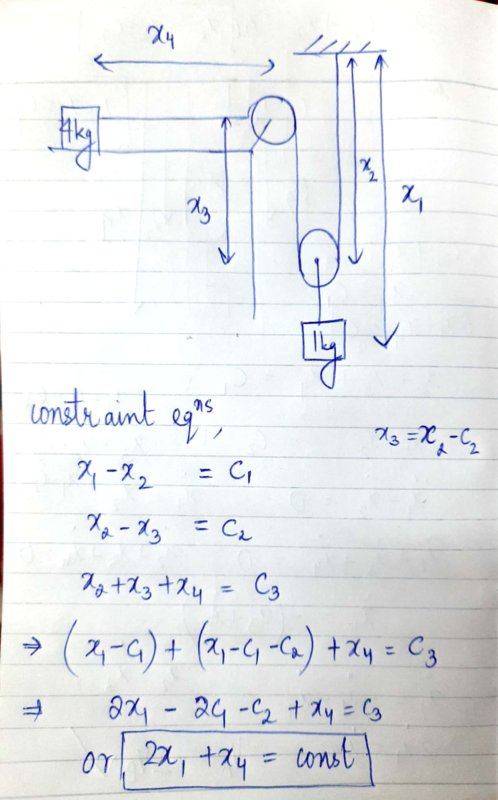
See the solved example as shown in the image. I don't understand how can we write S(A)=2S(B) since integrating V(A)=2V(B) will give us an extra unknown constant and the work done by friction will depend on it.

Relevant Equations

Work-Energy theorem & constraint equations.

See the solved example as shown in the image. I don't understand how can we write S(A)=2S(B) since integrating V(A)=2V(B) will give us an extra unknown constant and the work done by friction will depend on it. I found the relation 2S(B) + S(A) = const. (somebody confirm if this is right?) so isn't it technically wrong to say that S(A)=2S(B)?

 

[TSny]

$S_A$ and $S_B$ are displacements of the masses. $x_1$ and $x_4$ are positions of the masses.
In particular, $S_A = -\Delta x_4$ and $S_B = \Delta x_1$.

From your equation $2x_1+x_4 = \rm const$, derive a relation between $\Delta x_1$ and $\Delta x_4$.

 

[Merlin3189]

"I don't understand how can we write S(A)=2S(B) since integrating V(A)=2V(B) will give us an extra unknown constant "
No it won't. You have an obvious boundary condition that , when V(A)=0 , then V(B)=0.

 

[nish95]

@TSny, thank you very much for clarifying!

 

[Lnewqban]

I don't understand how can we write S(A)=2S(B)

The pulley to which mass B is attached, works as a lever.
Imagine the fulcrum of that lever located at the point where the right-hand vertical section of rope meets the pulley, the left-hand section of vertical rope lifting the weight B, which is located exactly midway between those two vertical sections of rope.
The mechanical advantage of such lever is 2.
The old "golden rule" of mechanics states that whatever you gain in force you lose in displacement.

Please, see:
http://www.technologystudent.com/gears1/pulley9.htm

https://en.wikipedia.org/wiki/Mechanical_advantage#Block_and_tackle

https://en.wikipedia.org/wiki/Simple_machine#Ideal_simple_machine

I believe that the relations you have established among the different Xs are incorrect, except the one that shows that the total length of the rope $(X_2+X_3+X_4)$ remains constant.