Block and pulley on movable incline

[Aurelius120]

Homework Statement

In the given figure if acceleration of Mass M with respect to ground is a then, find the acceleration of mass, m with respect to incline and with respect to the ground in terms of 'a'

Relevant Equations

T - Tcosα + Nsinα = Ma
mgsinα - T = ma
N = mgcosα

This was the question:

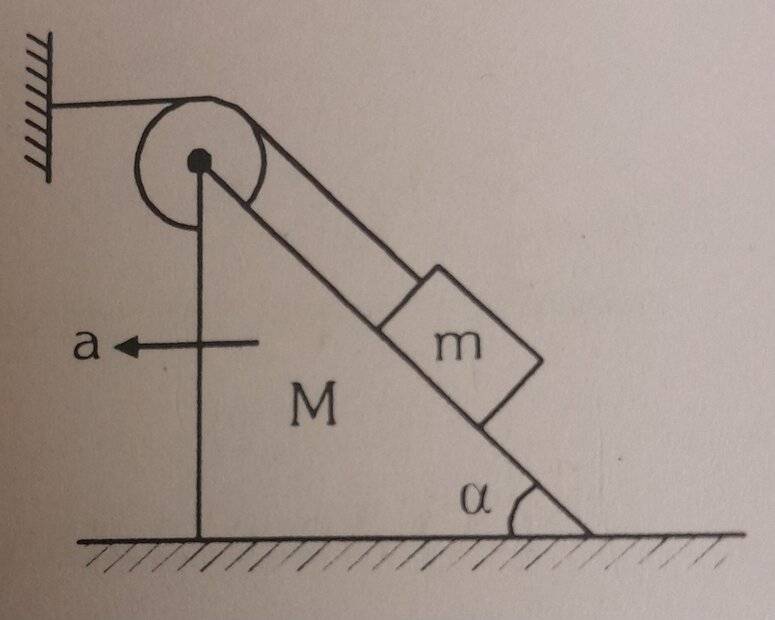
I derived the equations as mentioned in the relevant equations.

But I could not solve the equations to find the answer. I realise with respect to inclined plane the acceleration must be a since string cannot slack. With respect to ground, the acceleration of incline is added.

However, I could solve the force equations to get required acceleration. Other answers seem to ignore the effect of tension on the pulley due to pulley and use the former method.

What is the acceleration of the string in the ground frame? In the frame of the incline the acceleration on either side of pulley is equal and string does not slack.

In the ground frame, the string on the side of the block will get an horizontal component of acceleration but the fixed end of the string will have same acceleration. This implies the string should slack which it does not. So where is my mistake?How do I solve the problems using the force equations I derived?
Are my force equations correct.

 

[erobz]

$N$ doesn't equal $mg\cos \alpha$, the wedge has a component of its acceleration opposite the direction of the normal force acting on the hanging mass. Imagine the wedge to be moving away (effectively falling out from underneath it) from the hanging mass. Likewise, I suspect you must also be more careful in your force balance on the hanging mass parallel to the slope. If you were on the ground you would see the hanging mass accelerating down the slope, and with the wedge.

A couple FBD's a preferable here to just writing down some equations

 

[haruspex]

mgsinα - T = ma

The acceleration of the wedge has a component parallel to the slope. The sum of the real forces on the block parallel to the slope gives the acceleration of the block parallel to the slope in the ground frame, not in the wedge frame.
If you want to use the wedge frame you must add the inertial "virtual" force.