member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For A.1 of this problem,
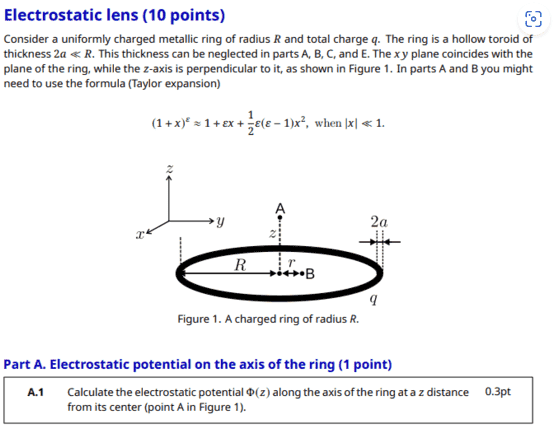
The solution is
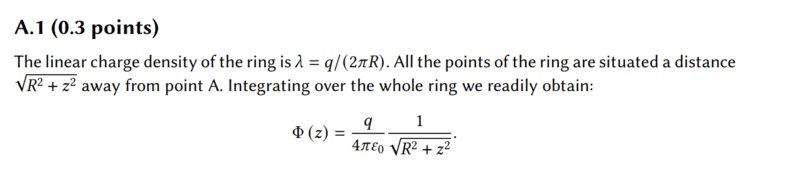
However, I have a doubt about the linear charge density ##\lambda##.
I don't understand how ##\lambda = \frac {q}{2\pi R} ## since this is not a thin ring, but has a non-negligible width of ##2a##
I think that the toroid has a larger area than thin circle with a circumference ##2\pi R## so linear charge density should be less than that expression.
EDIT: How would we calculate the electric potential if the thickness was not neglected?
Many thanks !
Problem from:
https://www.ipho2021.lt/uplfiles/Th2.pdf
https://www.ipho2021.lt/uplfiles/Th2-Solution.pdf
The solution is
However, I have a doubt about the linear charge density ##\lambda##.
I don't understand how ##\lambda = \frac {q}{2\pi R} ## since this is not a thin ring, but has a non-negligible width of ##2a##
I think that the toroid has a larger area than thin circle with a circumference ##2\pi R## so linear charge density should be less than that expression.
EDIT: How would we calculate the electric potential if the thickness was not neglected?
Many thanks !
Problem from:
https://www.ipho2021.lt/uplfiles/Th2.pdf
https://www.ipho2021.lt/uplfiles/Th2-Solution.pdf
Attachments
Last edited by a moderator:
