ago01
- 46
- 8
- Homework Statement
- Three masses, each 1 kg, are on a frictionless track with an immovable wall to the right. The left-most mass approaches the other two at 1 m/s. The masses will experience elastic collisions with each other and the wall, except velcro will cause the two on the right to stick together (see drawing). At what speed will the left-most mass ultimately move to the left in m/s?
- Relevant Equations
- mv, 1/2mv^2
Drawing:
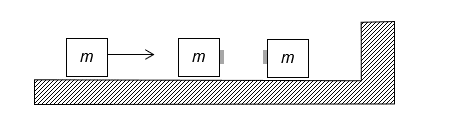
I decided to attempt to approach this as several collisions. So we can start with this:
Object 1-Object 2
This collision is elastic, so we know that ##P_i = P_f##. We also know ##K_i = K_f##.
So,
$$mv_{1i} = mv_{1f} + mv{2_f}$$
$$1 = v_{1f} + v_{2f}$$
$$v_{2f} = 1 - v_{1f}$$
and
$$1 = v_{1f}^2 + v_{2f}^2$$
Substituting these together we get:
$$1 = v_{1f}^2 + (1 - v_{1f})^2$$
and solving this quadratic equation we get that ##v_{1f} = 0## or ##v_{1f} = 1## and we can discard the 1 m/s result because we know that object 1 will transfer all of it's kinetic energy to object 2.
So, then it must be that ##v_{2f} = 1##.
Object 2 - Object 3
Now here is where I get a non-nonsensical result and I'm unsure how to proceed as continuing with this produced a final collision result equation that was absurd.
This collision again is elastic, but with the added fun of velcro. We proceed much the same way.
$$mv_{2i} = 2mv_f$$
and we immediately see the final velocity:
$$\frac{1}{2}v_{2i} = v_f$$
and substituting the previous result:
$$v_f = \frac{1}{2}$$
But when plugged into the kinetic energy equation things stop making sense (I did this to check my logic):
$$\frac{1}{2}mv_{2i}^2 = \frac{2m}{2}v_f^2$$
$$v_f = \sqrt{\frac{1}{2}v_{2i}^2} = \frac{1}{\sqrt{2}}v_{2i}$$
So I got two different results. Supposing this collision is elastic these should be conserved...so I am lost.
Object 2-3 Object 1
I was unable to proceed because I got two different results above. But I will walk through my reasoning for this part so you know that I tried it (I ended up trying to solve it and got no where that made sense and unfortunately erased my work).
Since the collision is once again elastic, we know that the combined mass will collide with the wall and bounce. So under conservation of momentum this will now have a velocity equal to ##-v_f## from the previous equation. Supposing this collides with the (now) stationary first object then this should be transferred entirely to the final mass.
If I can get the second part, and the third part's logic makes sense I think I can solve this. But I could use some pointers at where I have gone wrong so far.
Thank you!
I decided to attempt to approach this as several collisions. So we can start with this:
Object 1-Object 2
This collision is elastic, so we know that ##P_i = P_f##. We also know ##K_i = K_f##.
So,
$$mv_{1i} = mv_{1f} + mv{2_f}$$
$$1 = v_{1f} + v_{2f}$$
$$v_{2f} = 1 - v_{1f}$$
and
$$1 = v_{1f}^2 + v_{2f}^2$$
Substituting these together we get:
$$1 = v_{1f}^2 + (1 - v_{1f})^2$$
and solving this quadratic equation we get that ##v_{1f} = 0## or ##v_{1f} = 1## and we can discard the 1 m/s result because we know that object 1 will transfer all of it's kinetic energy to object 2.
So, then it must be that ##v_{2f} = 1##.
Object 2 - Object 3
Now here is where I get a non-nonsensical result and I'm unsure how to proceed as continuing with this produced a final collision result equation that was absurd.
This collision again is elastic, but with the added fun of velcro. We proceed much the same way.
$$mv_{2i} = 2mv_f$$
and we immediately see the final velocity:
$$\frac{1}{2}v_{2i} = v_f$$
and substituting the previous result:
$$v_f = \frac{1}{2}$$
But when plugged into the kinetic energy equation things stop making sense (I did this to check my logic):
$$\frac{1}{2}mv_{2i}^2 = \frac{2m}{2}v_f^2$$
$$v_f = \sqrt{\frac{1}{2}v_{2i}^2} = \frac{1}{\sqrt{2}}v_{2i}$$
So I got two different results. Supposing this collision is elastic these should be conserved...so I am lost.
Object 2-3 Object 1
I was unable to proceed because I got two different results above. But I will walk through my reasoning for this part so you know that I tried it (I ended up trying to solve it and got no where that made sense and unfortunately erased my work).
Since the collision is once again elastic, we know that the combined mass will collide with the wall and bounce. So under conservation of momentum this will now have a velocity equal to ##-v_f## from the previous equation. Supposing this collides with the (now) stationary first object then this should be transferred entirely to the final mass.
If I can get the second part, and the third part's logic makes sense I think I can solve this. But I could use some pointers at where I have gone wrong so far.
Thank you!