amylostorm
- 5
- 0
A few rules are commonly taught when dealing with problems regarding charge distributions of multiple charged plates/sheets at specified distances from each other(the sheets have infinite size) -
Now for my question, what exactly would grounding mean in such a system? Is it at 0V with respect to something? Or did we assume it as our reference potential? If we did the latter then I think the solution to these problems would also depend on its "absolute potential" as in say we have n plates with charges ## Q_1 , Q_2 ,..., Q_n ## and we connect one of these to a conducting hollow sphere far enough that it is not affected by the fields of this system. This is our ground. Then depending upon its potential(##\frac{kq_{sphere}}{R}##) wouldn't the sum of the charges on all the plates differ from zero? If it had a very high potential then it would force positive charge into the plate even if ## \sum Q_i ## was already positive. This could be done even while respecting the ## E=0 ## condition of all the plates. eg -
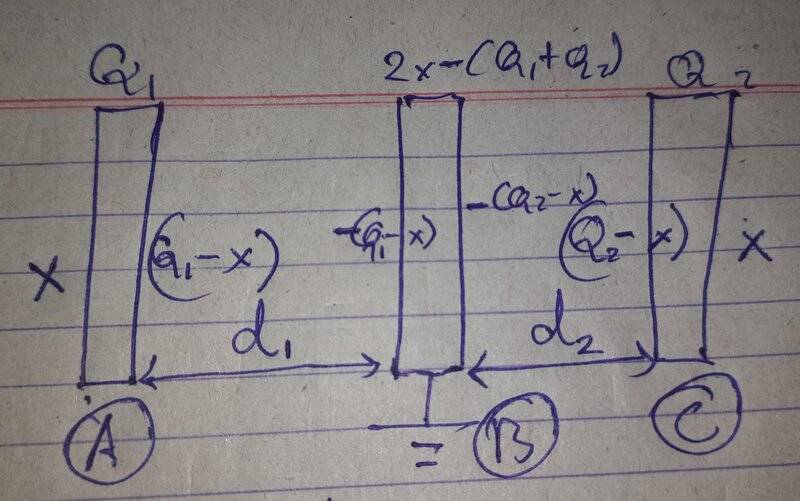
By varying x in these any amount of positive charge could be delivered into B while also having the fields cancel out inside of all conductors.
Tl;DR - explain a ground's potential and function in the context of infinite charged plates and prove that the sum of charges of all plates must be zero if one of them is grounded.
- Any two sheets facing each other must have opposite charges equal in magnitude on the inner faces
- The outer-most faces of the outer-most sheets must have charge equal to half the sum of all the charges distributed on all plates
- When any one sheet is "grounded", the sum of the charges of all plates becomes zero, thus the charge on the outer-most faces of the outer-most sheets is also zero
Now for my question, what exactly would grounding mean in such a system? Is it at 0V with respect to something? Or did we assume it as our reference potential? If we did the latter then I think the solution to these problems would also depend on its "absolute potential" as in say we have n plates with charges ## Q_1 , Q_2 ,..., Q_n ## and we connect one of these to a conducting hollow sphere far enough that it is not affected by the fields of this system. This is our ground. Then depending upon its potential(##\frac{kq_{sphere}}{R}##) wouldn't the sum of the charges on all the plates differ from zero? If it had a very high potential then it would force positive charge into the plate even if ## \sum Q_i ## was already positive. This could be done even while respecting the ## E=0 ## condition of all the plates. eg -
By varying x in these any amount of positive charge could be delivered into B while also having the fields cancel out inside of all conductors.
Tl;DR - explain a ground's potential and function in the context of infinite charged plates and prove that the sum of charges of all plates must be zero if one of them is grounded.