I Does the statistical weight of data depend on the generating process?

[PeroK]

but if they use it for statistical inference in such a manner that Bayes theorem replaces the frequentist definition of probability then they are de facto doing Bayesian statistics while merely pretending not to.

This is just pointless semantics. It's a pure coincidence that Bayes theorem (which is a simple set-theorectic result) shares a name with Bayesian statistical methods.

If Bayes' theorem had been called the law of equal areas, we wouldn't even be having this argument.

Even if we accept that Bayes theorem is part of Bayesian statistics, then the debate is simply between "type A statistical methods and "type B" statistical methods.

But, fundamentally, you cannot simply remove a key theorem from a mathematical structure. It's a bit like trying to commandeer the quadratic formula and saying: you can do your mathematics but you can't use the quadratic formula.

You can prove the quadratic formula from the axioms of algebra; and you can prove Bayes theorem from the axioms of set theory. You cannot just remove a theorem. Even if you try to take it away, what do you do when I prove it again the next day?

How do you stop me using Bayes' theorem, even if I never call it by name and never write it down explicitly? I can just allow the rules of set theory to do the work. Just like I could without ever using the quadratic formula. It would just happen in the background.

In fact, I like using the probability tree method. Bayes' theorem does in fact fall out of that and usually I haven't used it explicity.

This is absurd!

 

[Auto-Didact]

Again, the only question of relevance is if the definition of probability is implicitly changed from frequentist probability to Bayesian probability when a frequent uses Bayes theorem for statistical inference. If the answer is yes, then one is doing Bayesian statistics - at least in that single moment - whether they acknowledge it or not.

The only reason Bayesian probability and statistics exist as a separate mathematical framework is because the definition of probability is Bayes theorem in these mathematical frameworks. It is also important to realize that Bayesian probability theory invented by Laplace precedes frequentist probability theory invented by Quetelet, and that the latter is a limiting case of the former.

 

[Stephen Tashi]

There is a distinction between a mathematical model in which a certain quantity (e.g. the mean weight of a population of people) is "fixed, but unknown" and a model where that value is a realization of a random variable. In frequentist statistical models, the fundamental quantities that are unknown are modeled as "fixed, but unknown". In such a model, it makes no sense to talk about a "fixed, but unknown" quantity having some probability (different than 1 or zero) of having a given property. For example, if a population mean $\mu$ is "fixed but unknown" than it makes no sense to assign a probability of 0.95 of that mean being in the interval [ 31 - 8.2, 31 + 8.2].

The sense in which frequentist statistics does not recognize Bayes Theorem is that frequentist statistics uses models that do not recognize any probability distribution applying to the unknown quantities of principal interest. Hence no theorem about the probabilities of random variables can be applied to such quantities.

 

[Stephen Tashi]

@Stephen Tashi Given all that you said in post #129, what is your answer to the question posed in the OP?

Let's start with the question of whether a given value of $p$ assigns the outcome different probabilities in the two different experiments.

We have two couples, each of which has seven children that, in order, are six boys and one girl (i.e., the girl is the youngest of the seven).

Couple #1 says that they decided in advance to have seven children, regardless of their genders (they think seven is a lucky number).

Couple #2 says that they decided in advance to have children until they had at least one of each gender (they didn't want a family with all boys or all girls).

Consider the sex of a child to be the same independent random variable on each birth, and in both types of experiments.

In an experiment conducted by couples of type #1, the outcome "six boys born followed by 1 girl" has probability $p^6 (1-p)$.

In an experiment conducted by couples of type #2, after the initial birth, we use a geometric distribution to model the number of trials that occur until to the first "success", which is a birth of the other gender. There is a probability of $p$ that first birth is a boy. There is a probability of $p^5 (1-p)$ that we have "success" on the 7th birth. So the probability of the particular outcome "six boys born followed by a girl" is also $p^6 (1-p) = (p) (p^5)(1-p)$.

However, this does not say that experiments of type #1 and type #2 have the same probability of providing equal evidence about $p$. To compare an experiment of type #1 to an experiment of type #2 as experimental designs, we'd have to do a calculation where each possible outcome of the experiments is considered and define what would make one experiment type better than the other.

As far as hypothesis testing goes, both Bayesians and frquentists do calculations that consider more than one particular outcome. For example, in post #6, @PeroK, proposes a frequentist hypothesis test which considers outcomes without regard to order of birth and outcomes with "6 or 7" boys. Similarly, we see "one tailed" and "two tailed" tests being used. How do we justify such designs? It requires sophisticated thinking to do it rigorously.

 

[atyy]

There is a distinction between a mathematical model in which a certain quantity (e.g. the mean weight of a population of people) is "fixed, but unknown" and a model where that value is a realization of a random variable. In frequentist statistical models, the fundamental quantities that are unknown are modeled as "fixed, but unknown". In such a model, it makes no sense to talk about a "fixed, but unknown" quantity having some probability (different than 1 or zero) of having a given property. For example, if a population mean $\mu$ is "fixed but unknown" than it makes no sense to assign a probability of 0.95 of that mean being in the interval [ 31 - 8.2, 31 + 8.2].

The sense in which frequentist statistics does not recognize Bayes Theorem is that frequentist statistics uses models that do not recognize any probability distribution applying to the unknown quantities of principal interest. Hence no theorem about the probabilities of random variables can be applied to such quantities.

Take a probability distribution p(x,y) and model it parametrically using fixed but unknown parameters.

It is correct to state p(x,y) = p(x)p(x|y) = p(y)p(y|x), from which Bayes's rule follows.

 

[PeterDonis]

Bayes's rule is part of both Frequentist and Bayesian methods.

I agree this ought to be true; I'm not sure it actually is. I don't see frequentists emphasizing Bayes' rule; I see them emphasizing p-values. That's why I gave an example of a case where p-values and Bayes' rule give diametrically opposed answers as far as what should be told to a patient.

 

[PeterDonis]

Let's start with the question of whether a given value of pp assigns the outcome different probabilities in the two different experiments.

You can start wherever you like (everything that you said about p-values and probabilities has already been said multiple times in this thread), but I am asking you where you end up: what is your answer to the question posed in the OP? I didn't see one in your post.

 

[PeroK]

I agree this ought to be true; I'm not sure it actually is. I don't see frequentists emphasizing Bayes' rule; I see them emphasizing p-values. That's why I gave an example of a case where p-values and Bayes' rule give diametrically opposed answers as far as what should be told to a patient.

You could change an axiom of probability theory, but you can't arbitrarily remove a theorem just because it's got someone's name on it. If you want to do statistics without Bayes' theorem, then you'd have to fundamentally change the way probabilities work. They couldn't be based on set theory.

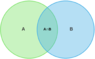
What Bayes' theorem says is that you can measure the intersection of two sets, $A$ and $B$ in two ways:

$P(A \cap B) = P(B|A)P(A) = P(A|B)P(B)$

Which says: the area of $A \cap B$ equals both:

The proportion that $A \cap B$ is of set $A$ ($P(B|A)$) times the area of $A$
The proportion that $A \cap B$ is of set $B$ ($P(A|B)$) times the area of $B$

This is illustrated by:



This is a fundamental theorem of probability theory. It's hard to avoid! It must be true.

That said, it's often given in the form:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

And can be presented as something quite deep and unintuitive. Even to the point where those with a political axe to grind could convince an intelligent man like yourself that it might even be contentious!

Now, some of the consequences of Bayes' theorem are not quite so intuitive. In every elementary probability course the classic example - normally using an example from disease testing - is covered. In fact, in the years I've been homework helping on PF this has come up several times.

A test for a certain disease has a 1% rate of false positives and a 0% rate of false negatives. If someone tests positive, what is the likelihood they have the disease?

And, the unwary first-year student might fall into the trap of immediately saying 99%.

The answer is, of course, that you have to do the maths (as they say) and it depends on how many of the population has the disease. If no one has the disease, then all positives are false; and, if everyone has the disease then all negatives are false. So, you also need an estimate of how many people in general have the disease. Let's say 0.5%.

I actually prefer the probability tree approach (and if you compel me not to use Bayes' theorem, I can always do it this way in any case and never mention the B-word):

Of the 0.5% who have the disease, all test positive.

Of the 99.5% who do not have the disease, 1% of these, which is approximately 1% of the total, test postive.

That gives us 3 positives out of 200 tests, with 1 having the disease and 2 being false positives. That leaves approximately a 1/3 chance that the person has the disease, given they tested positive.

Or, using Bayes' theorem explicitly:

A = person has the disease; B - person tests positive; $P(B|A) = 1$, $P(A) = 0.005$

First, you need to calculate $P(B)$:

$P(B) = P(A)P(B|A) + P(A')P(B|A') = (0.005)1 + (0.995)(0.01) = 0.01495$

Then, we can apply Bayes' theorem:

$P(A|B) = \frac{P(B|A)P(A)}{P(B)} = \frac{0.005}{0.01495} = 0.334$

Hence, just two ways to calculate the same number. Note that I think it illustrates how slick a method the probability tree can be.

Note that although Bayes' theorem explicity has the concept of prior $P(A)$ and posterior $P(A|B)$ in a formula, the same concepts are implicit in the probability tree approach. These concepts are not exclusive to Bayesian statistical methods: they appear naturally out of any probability calculations.

Note that the p-value is a measure of a parameter associated with a distribution and simply not appropriate here. This is, actually, the crux of the matter:

Given the assumptions about the distribution, you get a clear unambiguous answer about the likelihood that a person has the disease.

Given a new piece of data (new patient), there are statistical methods that calculate the effect on the prior distribution.

In other words, anyone who applies a p-value to a patient has simply got their statistical wires crossed. If you are telling me that clinicians with some statistical training do this, I can well believe it.

 

[Dale]

I hope you agree that there is a huge difference between Bayes theorem appearing as an extratheoretical purely mathematical consequence of set theoretical intersections and (the functions in) Bayes theorem serving as the definition of probability; only the latter is Bayesian probability theory.

As far as I know both Bayesians and frequentists both use the Kolomgorov axioms as the definition of probability and then Bayes theorem follows equally from the same axioms for both approaches. Since both camps accept the same axioms and theorems I don’t see “a huge difference” at all.

To me the difference between Bayesian probability and frequentist probability seems to be merely the interpretation of probability as long term frequencies for frequentists and as degrees of belief for Bayesians. As you probably know from other conversations I am not a big “interpretations” guy, so I am happy to use either interpretation as needed, even jumping between interpretations mid-calculation.

More practically, I would classify frequentist methods as those that compute probabilities of data given hypotheses and Bayesian methods as those that compute probabilities of hypotheses given data. But Bayes theorem applies either way, and a single person may use both types of methods as needed.

Again, a certain formula appearing as an application when doing mathematics and a certain formula being the central definition of the theory are clearly two different things.

Different maybe. But if the two camps accept the same mathematical statements as true then they are mathematically equivalent. I am ok with philosophically different but mathematically equivalent.

 

[PeroK]

As far as I know both Bayesians and frequentists both use the Kolomgorov axioms as the definition of probability and then Bayes theorem follows equally from the same axioms for both approaches. Since both camps accept the same axioms and theorems I don’t see “a huge difference” at all.

To me the difference between Bayesian probability and frequentist probability seems to be merely the interpretation of probability as long term frequencies for frequentists and as degrees of belief for Bayesians. As you probably know from other conversations I am not a big “interpretations” guy, so I am happy to use either interpretation as needed, even jumping between interpretations mid-calculation.

More practically, I would classify frequentist methods as those that compute probabilities of data given hypotheses and Bayesian methods as those that compute probabilities of hypotheses given data. But Bayes theorem applies either way, and a single person may use both types of methods as needed.

Absolutely! I was trying to say something like this.

 

[Dale]

Absolutely! I was trying to say something like this.

As an example of what I am talking about, IMO it is perfectly reasonable for a person to collect some appropriate data $D$ and use a traditional t-test to calculate $P(D|H_0)=0.001$ and then consider that to represent a low degree of belief in $D|H_0$.

Does that make him or her a Bayesian or a frequentist? They used a frequentist method and a Bayesian interpretation of the resulting probability. Maybe they are just a person doing statistics and don’t need to be pigeonholed into either camp.

Similarly, if I do an experiment and use Bayesian methods to construct $P(H|D)$ I could interpret that as a long run frequency of $H|D$ over an infinite number of repetitions of the experiment.

 

[atyy]

The big difference between a Bayesian and a Frequentist is that the former is coherent (a technical term), and the latter not necessarily so (uses common sense)

http://mlg.eng.cam.ac.uk/mlss09/mlss_slides/Jordan_1.pdf
•Coherence and calibration are two important goals for statistical inference
•Bayesian work has tended to focus on coherence while frequentist work hasn’t been too worried about coherence–the problem with pure coherence is that one can be coherent and completely wrong
•Frequentist work has tended to focus on calibration while Bayesian work hasn’t been too worried about calibration–the problem with pure calibration is that one can be calibrated and completely useless
•Many statisticians find that they make use of both the Bayesian perspective and the frequentist perspective, because a blend is often a natural way to achieve both coherence and calibration

 

[Auto-Didact]

As far as I know both Bayesians and frequentists both use the Kolomgorov axioms as the definition of probability and then Bayes theorem follows equally from the same axioms for both approaches. Since both camps accept the same axioms and theorems I don’t see “a huge difference” at all.

As I have addressed here and here being derivable from Kolmogorov axioms, while nice, is almost completely vacuous when approaching the matter from a rigourously justifiable foundational perspective; the axiomatic formulation fails to be exactly that. To quote John Bell: If you make axioms, rather than definitions and theorems, about the ‘measurement’ of anything else, then you commit redundancy and risk inconsistency.

As an example of what I am talking about, IMO it is perfectly reasonable for a person to collect some appropriate data $D$ and use a traditional t-test to calculate $P(D|H_0)=0.001$ and then consider that to represent a low degree of belief in $D|H_0$.

Does that make him or her a Bayesian or a frequentist? They used a frequentist method and a Bayesian interpretation of the resulting probability. Maybe they are just a person doing statistics and don’t need to be pigeonholed into either camp.

Similarly, if I do an experiment and use Bayesian methods to construct $P(H|D)$ I could interpret that as a long run frequency of $H|D$ over an infinite number of repetitions of the experiment.

Let's make an analogy: suppose someone is doing Newtonian mechanics and needs to calculate the momentum, but then instead of using the Newtonian definition for the momentum he momentarily steps out of Newtonian theory, borrows the definition of momentum from special relativity and then uses this definiton instead, and then just returns to Newtonian theory and carries out the rest of the analysis completely conventionally.

It should be clear that this is a schizophrenic way of doing Newtonian mechanics; in the same manner performing a bait and swap of the definition of probability by importing another definition based on Bayes theorem - i.e. the definition of probablity from Bayesian probability - and then doing the rest of the analysis in the frequentist manner is a schizophrenic way of doing frequentist statistics.

To use a less acerbic tone, performing such an unjustified switch is de facto engaging in a mathematically inconsistent procedure. In fact this mathematical inconsistency is fully analogous to Penrose' description of the measurement problem in QM where sometimes $\psi$ evolves via unitary evolution, while other times $\psi$ progresses via state vector reduction.

The big difference between a Bayesian and a Frequentist is that the former is coherent (a technical term), and the latter not necessarily so (uses common sense)

http://mlg.eng.cam.ac.uk/mlss09/mlss_slides/Jordan_1.pdf
•Coherence and calibration are two important goals for statistical inference
•Bayesian work has tended to focus on coherence while frequentist work hasn’t been too worried about coherence–the problem with pure coherence is that one can be coherent and completely wrong
•Frequentist work has tended to focus on calibration while Bayesian work hasn’t been too worried about calibration–the problem with pure calibration is that one can be calibrated and completely useless
•Many statisticians find that they make use of both the Bayesian perspective and the frequentist perspective, because a blend is often a natural way to achieve both coherence and calibration

This is highly analogous to the difference between a mathematician and a physicist who approach the issue of constructing models based on different goals, namely precision versus accuracy; for the physicist having an extremely precise but inaccurate model is useless, while for the mathematician engaging in modelling, precision of formulation as well as obtaining solutions tends to be key while accuracy of the model tends to be only of secondary concern.

 

[PeterDonis]

Let's make an analogy

A bad one. In your analogy, you're changing the math. You're not reinterpreting the Newtonian momentum to mean something else; you're removing the Newtonian momentum and replacing it with the SR momentum, which is a different mathematical expression.

In the post by @Dale that you quoted, the math is the same in both cases; the only difference is in interpretation of what the math means.

 

[Auto-Didact]

A bad one. In your analogy, you're changing the math. You're not reinterpreting the Newtonian momentum to mean something else; you're removing the Newtonian momentum and replacing it with the SR momentum, which is a different mathematical expression.

In the post by @Dale that you quoted, the math is the same in both cases; the only difference is in interpretation of what the math means.

That is my point: the semantic definition of probability in frequentist probability theory is relative frequency. On the contrary, the fact that this semantic definition can be swapped out and replaced for the Bayesian definition without immediately breaking all the mathematics (see John Baez' extensive postings on this topic in his blog/publications) is actually suggestive that frequentist probability theory is actually a limiting case of Bayesian probability theory, making the analogy with Newtonian mechanics and SR even more apt.

On the other hand, the occurrence of Bayes' theorem (BT) in frequentist probability theory as described in the Wikipedia example about probability trees which was referred to earlier in the thread does not have BT in the role of defining the meaning of probability as it does in Bayesian probability. Instead the occurrence of BT there is a consequence of doing graph analysis, i.e. it arises as a solution when applying graph theory and/or set theory to probability theory.

This specific occurrence of BT can be viewed as analogous to the idealized problem in Newtonian mechanics where two block of specific masses collide with perfect elasticisty on a frictionless surface and a wall at one end, where the amount of collisions in this scenario happen to numerically approximate the digits of $\pi$; clearly this occurrence of $\pi$ here is in a sense a mathematical 'accident', which has very little to do with the specific essential content of Newtonian mechanics itself as a physical theory.

 

[PeterDonis]

That is my point

I wasn't questioning your point about interpretations of probability. I was questioning the analogy you gave.

is actually suggestive that frequentist probability theory is actually a limiting case of Bayesian probability theory, making the analogy with Newtonian mechanics and SR even more apt

No, the analogy is still a bad one for the reason I already gave.

 

[Dale]

is almost completely vacuous when approaching the matter from a rigourously justifiable foundational perspective

I am not concerned whatsoever about rigorously justifiable foundational perspectives.

As far as I know frequentists accept that the Kolomgorov axioms are true statements in the context of frequentist statistics. Similarly for Bayesians. Since Bayes theorem is derivable from the Kolomgorov axioms and since both camps accept the axioms as true statements then Bayes theorem is unambiguously part of both camps set of mathematical tools.

If your rigorously justifiable foundational perspective cannot see the observed fact that both Bayesians and frequentists actually do use Bayes theorem then you may need to get a new perspective.

Let's make an analogy: suppose someone is doing Newtonian mechanics and needs to calculate the momentum, but then instead of using the Newtonian definition for the momentum he momentarily steps out of Newtonian theory, borrows the definition of momentum from special relativity and then uses this definiton instead,

In that analogy the math is not the same.

A better analogy would be someone doing calculations in relativity using the Lorentz transform but switching between the block universe interpretation and the Lorentz aether interpretation. While you may call it schizophrenic it would be perfectly legitimate to do.

Frankly, your arguments seems to amount to some sort of intellectual name calling. Frequentists, to your view, cannot use Bayes theorem without being schizophrenic or losing rigorously justifiable foundations. So what? It works and because it works they use it.

 

[Auto-Didact]

Name calling as I said is not the intention as I already mentioned: I am explicitly calling out the mathematical inconsistency that blatantly occurs within the usage of the mathematical formalism; essentially Bayesians say probabilities are dynamical objects which can be updated using a conditional law, while frequentists say probabilities are objective and non-dynamical, i.e. relative frequencies. Either probabilities are things that can be updated or they cannot, one cannot have it both ways.

This is one of the longstanding problems in the foundations of probability theory. Moreover, this situation is fully analogous to the mathematical inconsistency committed when utilizing QM in practice, which is usually characterized as the measurement problem, which is of course the central problem in the foundations of QM. If one doesn't care about the measurement problem in the foundations of QM, they probably don't care about this issue either for exactly the same reasons.

Notice that the question of Bayesian/frequentist statistics is predicated upon the choice of Bayesian/frequentist probability theory. The problems of the practicing statistician is not reducible nor isomorphic to the problems of the practicing probability theorist, nor vice versa. Statistics is not probability theory and equivocating what the two camps think is where things start to go awry: this is the same reason engineers aren't theoretical physicists, nor vice versa.

As I already said, the key inconsistency is in the definition of what a probability is. Deciding the definition of what a probability is is not a matter for statisticians, but is a matter for mathematicians which work in the foundations of probability theory, i.e. mathematicians who create new probability theories. This is exactly analogous to theoretical physicists who come up with new theories of physics e.g. how SR is a theory of mechanics giving a new definition of motion which replaces another theory of mechanics which has another definition of motion.

The way to remove this inconsistency in the foundations of PT is to construct a new theory of probability which completely subsumes the old ones; in the process much of the foundations of mathematics and logic tend to be uprooted as well, indicating that this is an enormously difficult foundational issue in mathematics. There are many proposals and new generalized theories of probability but these are so far mostly academic, with very specific applications in specific widely diverse scientific fields.

Finally, Kolmogorovian probability theory is completely useless in solving this issue because it doesn't suggest how to proceed in solving the open problem, but instead merely tells us that the older inadequate theories can be formalized; this is like telling Newton when he was coming up with mechanics that Aristotelian mechanics can be reduced to some system of axioms.

Bringing up KPT in the discussion of the definition of probability is as useful as telling a theoretical physicist searching for the quantum theory of gravity that there already exists an axiomatic formulation of SR-based QFT and therefore he should stop searching. People who continue to bring up KPT in this discussion do not realize that they haven't even understood the basic issue at all; they should educate themselves before engaging in this centuries long discussion.

 

[PeterDonis]

I am explicitly calling out the mathematical inconsistency that blatantly occurs within the usage of the mathematical formalism

It can't be a mathematical inconsistency with one and not the other if both are using the same math. @Dale has already pointed out that both frequentists and Bayesians accept the Kolmogorov axioms, and Bayes' Theorem follows logically from them. So there is no mathematical inconsistency with both of them accepting Bayes' Theorem and using it.

The way to remove this inconsistency in the foundations of PT is to construct a new theory of probability

PF is not for discussion of original research. If you think this needs to be done, go and do it and publish a peer-reviewed paper on it.

You have now been banned from further posting in this thread.

 

[Dale]

I am explicitly calling out the mathematical inconsistency that blatantly occurs within the usage of the mathematical formalism

I am not convinced that there is a mathematical inconsistency. Which of Kolomgorov’s axioms are inconsistent with the other? If the axioms are not inconsistent with each other then a theorem derived from them is also not mathematically inconsistent. If there is a mathematical inconsistency then it is certainly not blatant.

Perhaps you mean some sort of philosophical or practical inconsistency where it is inconsistent to apply Kolomgorov’s axioms to long run frequencies. I don’t think such an inconsistency is blatant either, if it even exists.

Kolmogorovian probability theory is completely useless in solving this issue

Regardless of your dislike of the Kolomgorov axioms, they are used in a large number of standard statistical textbooks. A frequentist textbook using the Kolomgorov axioms is not being mathematically inconsistent to also use Bayes theorem, since the former implies the latter.

frequentists say probabilities are objective and non-dynamical, i.e. relative frequencies.

Do you have a reference for this? I don’t think this is a correct claim.

 

[PeterDonis]

Do you have a reference for this? I don’t think this is a correct claim.

Please note that this poster has been thread banned, so he can't respond here.

AFAIK frequentists do equate probabilities with frequencies, which are supposed to be objective (everyone should agree on what they are in a particular case), but the "non-dynamical" part IMO is that particular poster's personal speculation.

 

[Dale]

AFAIK frequentists do equate probabilities with frequencies, which are supposed to be objective (everyone should agree on what they are in a particular case), but the "non-dynamical" part IMO is that particular poster's personal speculation.

Yes, that is the part that I am skeptical about.

 

[Stephen Tashi]

You can start wherever you like (everything that you said about p-values and probabilities has already been said multiple times in this thread), but I am asking you where you end up: what is your answer to the question posed in the OP? I didn't see one in your post.

Do you realize that the original post does not pose a specific mathematical question?

You are asking me to make a series of subjective judgements in order to define "strength of evidence" and then solve a possibly hard mathematical problem using my own definitions. At the moment, I'm not inclined to exert myself to both to define the question and then solve it!

 

[PeterDonis]

You are asking me to make a series of subjective judgements in order to define "strength of evidence" and then solve a possibly hard mathematical problem using my own definitions.

First, I have given quite a bit of clarification in subsequent posts in this thread.

Second, whatever judgment you make, it should be the same for both couple #1 and couple #2; that is the only actual requirement. I did not ask you to actually quantify "strength of evidence" for either couple. I only asked you to say whether it is different for one couple as compared to the other. That is a simpler question since you can use general properties of possible measures of "strength of evidence" to answer it even without having to calculate them. For example, the straightforward Bayesian answer--same prior, same data, therefore same posterior--can be given without actually calculating any of those things.

At the moment, I'm not inclined to exert myself to both to define the question and then solve it!

Then I would appreciate it if you would refrain from further posting in this thread, since others who have posted here do not share your inclination.

 

[Dale]

You are asking me to make a series of subjective judgements in order to define "strength of evidence"

There is a standard definition for the strength of the evidence, which I cited for you above.