Engineering Electrical Engineering - Circuits - Transistors

[GreenPrint]

To say more about all this. Your method of solution reduced the 4 unknowns to 2 by taking advantage of the fact that you didn't want vc1 anyway, and that vs is a known since it is the node where we want to inject our input.

Setting your 2 KCL equations equal to each other is how you solved 2 simultaneous equations., with a considerable amount of algebra.

When you use a computer to solve systems of simultaneous equations, it's no harder to solve 20 simultaneous equations than it is to solve 2.

As an example, imagine that we want to improve the linearity of your circuit. We add a 50k ohm feedback resistor from vo to vb1; let there be a large capacitor in series with it to avoid upsetting the DC bias. You still have 4 nodes, but you will find that the problem becomes very much more complicated using the method you did.

But, if you have already got the system of 4 KCL equations set up, it's a trivial matter to add the feedback resistor, and let the computer do the additional work.

Here's the system with the feedback resistor added (in red); you can see that the additions to the equations are trivial. Solving the system with a linear solver by computer easily gives the result shown. Av is reduced by about a factor of 3. The only extra work to do is to add 4 elements to the system:

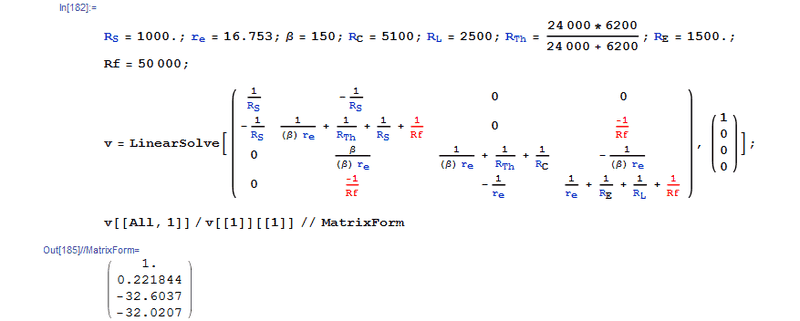
I know you're a busy student, but if you give a try to solving the circuit with feedback by hand, you'll appreciate just how much the addition of one more resistor complicates things.

Also where did you get R_{f} from? In my book it uses something like r_{O} every now and then as a output resistance of the transistor that is very large that it sometimes includes in problems and sometimes doesn't. Is this the same resistor?

 

[NascentOxygen]

Also where did you get R_{f} from?

The Electrician decided he would add a little spice to this rather bland problem, so he added an extra resistor to give feedback to (according to theory) improve the performance of your basic amplifier.

He changed the circuit just for fun. R_f is his feedback resistor ("We add a 50k ohm feedback resistor from vo to vb1").

 

[The Electrician]

Ya I think I made a mistake in my post, I met to say \frac{v_{O}}{v_{S}}.

I don't see how there is an error in my KCL equation for node v_{C_{1}}. I'll assume that all of the currents are flowing out of node, giving me
\frac{v_{s}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}} + \frac{v_{C_{1}}}{R_{C}||R_{Th}} + \frac{v_{C_{1}} - v_{E_{2}}}{βr_{e}} = 0
I factor the terms with v_{C_{1}}
\frac{v_{s}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}} + v_{C_{1}}(\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}) - \frac{v_{E_{2}}}{βr_{e}} = 0
move the terms without v_{C_{1}} to the RHS
v_{C_{1}}(\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}) = \frac{v_{E_{2}}}{βr_{e}} - \frac{v_{s}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}}
solve for v_{C_{1}}
v_{C_{1}} = (\frac{v_{E_{2}}}{βr_{e}} - \frac{v_{s}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}})(\frac{1}{(\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}})})

I don't really see what I'm doing wrong. the current through the second resistor of resistance βr_{e}, is the voltage across the resistor divided by the resistance.
i_{B_{2}} = \frac{v_{C_{1}} - v_{E_{2}}}{βr_{e}}<br />

Here's what you got in post #44:

v_{C_{1}} = (\frac{v_{E_{2}}}{βr_{e}} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})βr_{e}})\frac{1}{\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}}

And here's what you get in this post:

v_{C_{1}} = (\frac{v_{E_{2}}}{βr_{e}} - \frac{v_{s}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}})(\frac{1}{(\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}})})

Why the difference?

One problem I see is that the first subexpression at the beginning of your derivation:

\frac{v_{s}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}}

Doesn't have units of current. You might want to fix that and solve for vc1 again.

Believe it or not, this question appeared on of my examinations which I got wrong. I know that during a test I would rather much not solve this problem using algebra and that solving it using matrix would be much easier and allow for less errors. I could plug the values into my TI-84 and get the answers. I think perhaps it's a good idea to solve circuits like this by hand, but when it gets more complex it's just down right a waste of time, and when during an examination it doesn't make much sense to plug through the algebra.

I don't know just my thoughts.

You would be surprised how fast the solutions for network problems like this grow with the addition of just one or two more nodes, or additional parameters. The current problem is just about the limit of what you can reasonably do without the algebra becoming so cumbersome that it can't be done without mistakes.

Single transistors are often described at low frequencies with 4 parameters, hie, hfe, hre and hoe. In student problems it's almost universal that hre is taken to be zero (ignored, in other words), and typically, hoe (also known as ro) is taken to be zero. If, in your problem, hre had not been zero, your algebra would have been totally out of hand.

 

[GreenPrint]

Start off by defining v_{B_{1}}
v_{B_{1}} = \frac{v_{S}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}}
define the current i_{B_{1}}
i_{B_{1}} = \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})βr_{e}}
write KCL at node v_{C_{1}}
\frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})r_{e}} + \frac{v_{C_{1}}}{R_{C}||R_{Th}} + \frac{v_{C_{1}} - v_{E_{2}}}{βr_{e}} = 0
on the LHS move terms without v_{C_{1}} to the RHS and factor terms on the LHS that contain v_{C_{1}}
v_{C_{1}}(\frac{1}{R_{C}||R_{Th} + \frac{1}{βr_{e}}}) = \frac{v_{E_{2}}}{βr_{e}} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})r_{e}}
solve for v_{C_{1}}
v_{C_{1}} = (\frac{1}{\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}})(\frac{v_{E_{2}}}{βr_{e}} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})r_{e}})
factor out r_{e}
v_{C_{1}} = \frac{1}{r_{e}}(\frac{1}{\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}})(\frac{v_{E_{2}}}{β} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})})
simplify
v_{C_{1}} = (\frac{1}{\frac{r_{e}}{R_{C}||R_{Th}} + \frac{1}{β}})(\frac{v_{E_{2}}}{β} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})})

I don't see how the β cancels out but believe that the answer above is correct and don't see how it's not. Thanks I didn't realize that I forgot about the r_{e} previously in the current generator.

 

[The Electrician]

Start off by defining v_{B_{1}}
v_{B_{1}} = \frac{v_{S}(R_{Th}||βr_{e})}{R_{S} + R_{Th}||βr_{e}}
define the current i_{B_{1}}
i_{B_{1}} = \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})βr_{e}}
write KCL at node v_{C_{1}}
\frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})r_{e}} + \frac{v_{C_{1}}}{R_{C}||R_{Th}} + \frac{v_{C_{1}} - v_{E_{2}}}{βr_{e}} = 0
on the LHS move terms without v_{C_{1}} to the RHS and factor terms on the LHS that contain v_{C_{1}}
v_{C_{1}}(\frac{1}{R_{C}||R_{Th} + \frac{1}{βr_{e}}}) = \frac{v_{E_{2}}}{βr_{e}} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})r_{e}}
solve for v_{C_{1}}
v_{C_{1}} = (\frac{1}{\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}})(\frac{v_{E_{2}}}{βr_{e}} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})r_{e}})
factor out r_{e}
v_{C_{1}} = \frac{1}{r_{e}}(\frac{1}{\frac{1}{R_{C}||R_{Th}} + \frac{1}{βr_{e}}})(\frac{v_{E_{2}}}{β} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})})
simplify
v_{C_{1}} = (\frac{1}{\frac{r_{e}}{R_{C}||R_{Th}} + \frac{1}{β}})(\frac{v_{E_{2}}}{β} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})})

I don't see how the β cancels out but believe that the answer above is correct and don't see how it's not. Thanks I didn't realize that I forgot about the r_{e} previously in the current generator.

In post #47, I pointed out that you had a mistake in your first KCL equation for vc1 in post #44.. What you had was this:

The β in red shouldn't be there.

The derivation you show in post #54 obtains this result:

v_{C_{1}} = (\frac{1}{\frac{r_{e}}{R_{C}||R_{Th}} + \frac{1}{β}})(\frac{v_{E_{2}}}{β} - \frac{v_{S}(R_{Th}||βr_{e})}{(R_{S} + R_{Th}||βr_{e})})

This result is correct; it's not the same as the one I complained about. See how easy it is to make mistakes when doing so much algebra?

My point in post #47 was, if you had in fact used the incorrect expression for vc1, you wouldn't have obtained the correct final result for vo/vs. Yet, somehow you did. Obviously you used a correct expression for vc1, not the incorrect one you showed.

Now all you have to do is get the correct current gain, Ai.

 

[GreenPrint]

Oh ok thanks.

I can just use
A_{i_{T}} = -A_{v_{T}}\frac{Z_{i_{1}}}{R_{L}}

The input impedance of the first stage is just R_{Th}||βr_{e}

So

A_{i} = -A_{v}\frac{Z_{i}}{R_{L}} = 90.214 \frac{4.927 KΩ||2512.95 Ω}{2.5 KΩ} ≈ 60.052

Does this look correct?

 

[The Electrician]

Oh ok thanks.

I can just use
A_{i_{T}} = -A_{v_{T}}\frac{Z_{i_{1}}}{R_{L}}

The input impedance of the first stage is just R_{Th}||βr_{e}

So

A_{i} = -A_{v}\frac{Z_{i}}{R_{L}} = 90.214 \frac{4.927 KΩ||2512.95 Ω}{2.5 KΩ} ≈ 60.052

Does this look correct?

I thought your instructor had said that Av was to be calculated from the Vs point. To be consistent, you should also calculate Ai from that point, so the input impedance should be R_S+R_{Th}||βr_{e}

 

[GreenPrint]

So then when I take this into consideration I get about 1.066 so the current again is essential 1. Does this sound correct?

 

[The Electrician]

So then when I take this into consideration I get about 1.066 so the current again is essential 1. Does this sound correct?

I get:

A_{i} = -A_{v}\frac{Z_{i}}{R_{L}} = 90.214 \frac{1.0 kΩ+4.927 KΩ||2512.95 Ω}{2.5 KΩ} ≈ 96.138

 

[GreenPrint]

(\frac{1}{4927} + \frac{1}{2512.95})^{-1} ≈ 1664.165
1664.165 + 1000 ≈ 2664.165
\frac{2664.165}{2500} ≈ 1.066?